Topological Data Analysis
Gregory Clark
July 30, 2014
Topology is "Pure" Math

Our goal is to understand the shape of high-dimensional data better using topological tools.
Homotopy Groups
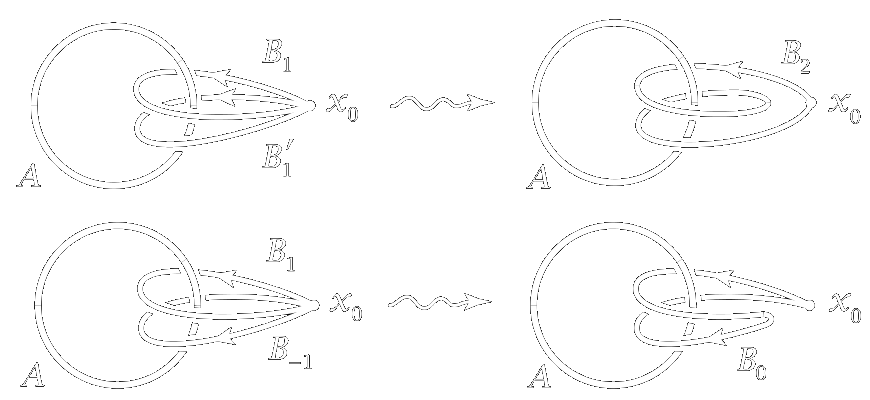
The corner stone algebraic topology, \(\pi_1\), is the group of equivalence classes of loops where two loops are equivalent if one can be continuously deformed into the other.
More generally, other homotopy groups are defined on equivalence classes of higher dimensional “loops” (maps from higher dimensional spheres).
These groups are topological invariants, and computing them would help us identify the shape of spaces. However, . . .
Intractible Computations
However, homotopy groups are notoriously difficult to compute (due to generator and relation computations in free groups). [Carlsson] [Hatcher]
Simplicial Homology
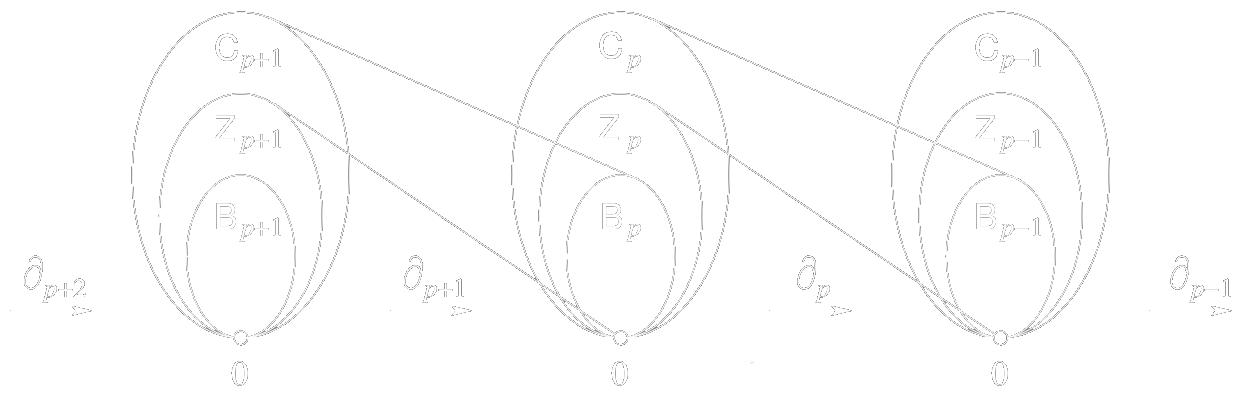
Homology groups are easier to compute.*
*Technical conditions apply.
Betti Numbers
The \(k^{\text{th}}\) Betti number is the number of generators of the \(k^{\text{th}}\) homology group.
We may calculate Betti numbers using the Smith normal forms of matrix represenations of the boundary operators \(\delta_i\).
The \(k^{\text{th}}\) Betti number counts equivalence classes of \(k\)-dimensional surfaces (the number of “\(k\)-dimensional holes”) in the space.
Wedge of Circles
For example, let \(X = S^1 \vee S^1\) be the wedge of two circles.

What are the Betti numbers of \(X\)?
| \(\beta_0 = \) | the number of connected components | \(= 1\) |
| \(\beta_1 =\) | the number of one-dimensional holes | \(= 2\) |
| \(\beta_k =\) | \( 0 \quad \text{ for all } k > 1\) |
Betti Numbers of a Dataset
Suppose we have a dataset containing \(n\) points in \(\mathbb{R}^d\).
What are the Betti numbers of that set?
| \(\beta_0 = \) | the number of connected components | \(= n\) |
| \(\beta_1 =\) | the number of one-dimensional holes | \(= 0\) |
| \(\beta_k =\) | \( 0 \quad \text{ for all } k > 0\) |
Okay, that’s fine... but not very interesting.
Simplicial Complexes
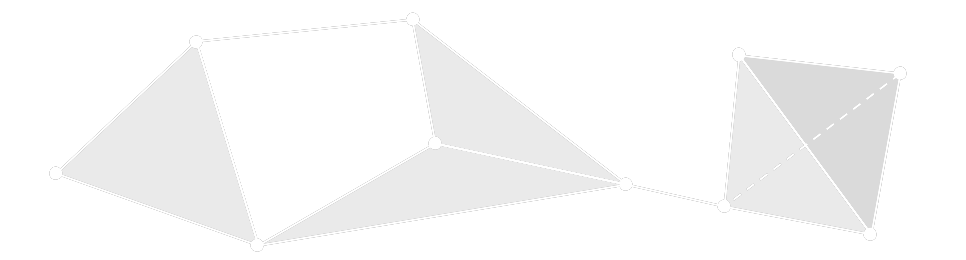
Simplicial complexes are generalizations of graphs.
Instead of edges that connect two vertices, simplicial complexes have simplices which connect any number of vertices.
A Formal Definition
The sets in \(A\) of cardinality \(k+1\) are called \(k\)-simplices.

We often blur the distinction between an abstract simplicial complex and its geometric realization in Euclidean space.
Čech Complex
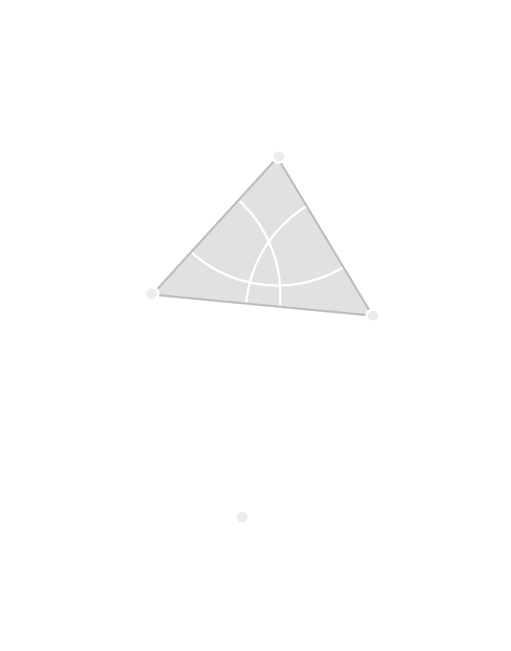
The Čech complex is the nerve of the balls of radius \(r\) around each point.

Vietoris-Rips Complex
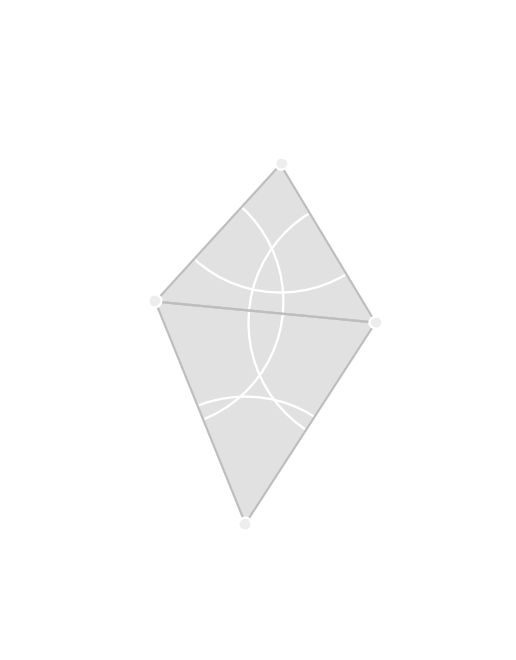
The Vietoris-Rips complex contains all edges between points that are within \(2r\) along with every higher-dimensional simplex whose edges are all included.

Vietoris-Rips Lemma
We tend to favor Vietoris-Rips complexes since they are easier to compute.
Caveat
Both Čech and Vietoris-Rips complexes could produce a simplicial complex of higher dimension than the space we started in!
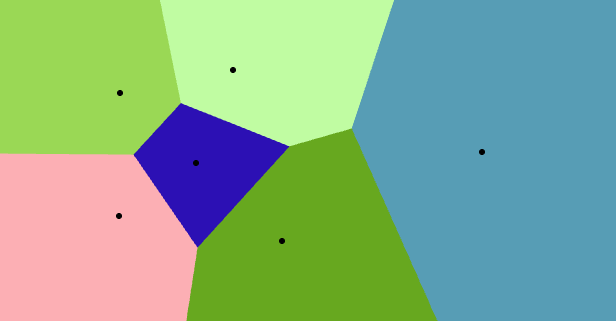
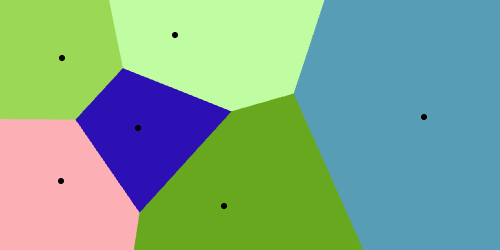
Delaunay Complex
Interactive Voronoi Diagram Generator
Alpha Complex
where \(R_u(r) = B_u(r) \cap V_u\).
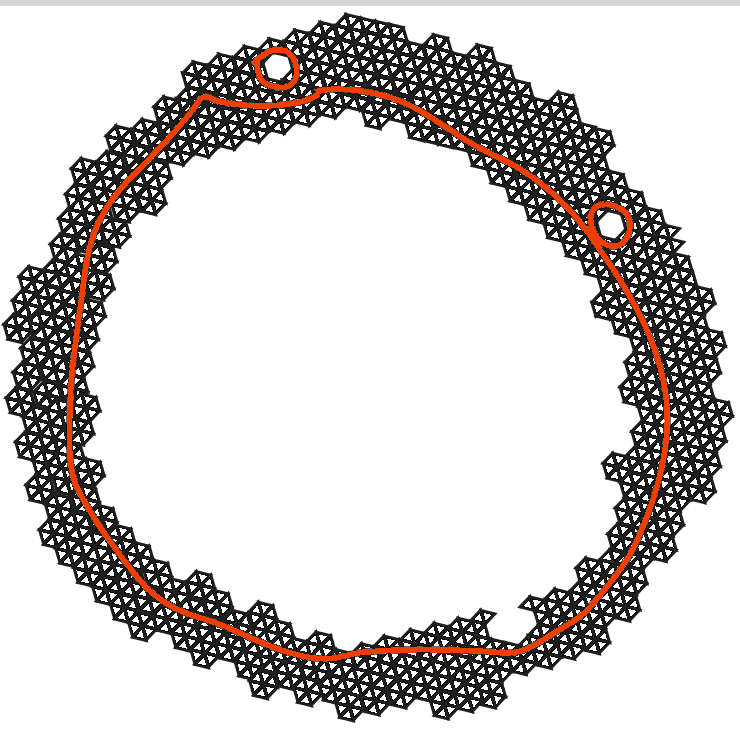
(Lazy) Witness Complex
In practice using all of the points in a dataset can be wasteful in terms of computing time and memory. The Witness construction strategically chooses landmark points and creates a simplicial complex that is (hopefully) still a faithful topological representation of the underlying space.
Lazy-Witness : Witness : : Vietoris-Rips : Čech
Another Caveat
Real world data is often messy, and chosing a particular radius \(r\) can yield a simplicial complex with artificial features.

Persistent Homology
The features that persist for a large range of resolutions are more likely to represent genuine features of the underlying space.
Software for TDA
Plex: Simplicial Complexes in Matlab
| Plex 2.5.1 | |
|---|---|
| Authors: | Patrick Perry Vin de Silva |
| Started: | 2000 |
| Updated: | 2006 (deprecated) |
| Language | files | blank | comment | code |
|---|---|---|---|---|
| C++ | 85 | 2709 | 3843 | 10206 |
| Bourne Shell | 6 | 843 | 1339 | 8280 |
| C/C++ Header | 74 | 1973 | 6499 | 5209 |
| MATLAB | 67 | 629 | 2165 | 2219 |
| m4 | 7 | 158 | 109 | 1110 |
| make | 17 | 109 | 53 | 206 |
| SUM: | 256 | 6421 | 14008 | 27230 |

JPlex: Persistent Homology Library
| JPlex (PLEX3) | |
|---|---|
| Authors: | Henry Adams John Chakerian |
| Started: | 2006 |
| Updated: | 2011 “phased out” |
| Language | files | blank | comment | code |
|---|---|---|---|---|
| HTML | 62 | 3048 | 1283 | 24667 |
| Java | 57 | 1674 | 6800 | 8969 |
| Bourne Shell | 4 | 816 | 1016 | 7759 |
| Bourne Again Shell | 1 | 69 | 88 | 570 |
| C++ | 1 | 175 | 30 | 370 |
| MATLAB | 9 | 106 | 398 | 309 |
| R | 2 | 44 | 5 | 170 |
| Ant | 1 | 20 | 0 | 143 |
| SUM: | 141 | 5977 | 9634 | 43020 |

JavaPlex: Persistent Homology Library
| javaPlex 4.2.0 | |
|---|---|
| Authors: | Andrew Tausz Mikael Vejdemo-Johansson Henry Adams |
| Started: | 2010 |
| Updated: | yesterday |
| Language | files | blank | comment | code |
|---|---|---|---|---|
| HTML | 405 | 15891 | 7715 | 130927 |
| Java | 259 | 5695 | 12620 | 23457 |
| Bourne Shell | 6 | 819 | 1016 | 7773 |
| MATLAB | 190 | 1769 | 1446 | 4656 |
| Bourne Again Shell | 1 | 69 | 88 | 570 |
| C++ | 1 | 175 | 30 | 370 |
| Ant | 1 | 32 | 11 | 223 |
| R | 2 | 44 | 5 | 170 |
| Arduino Sketch | 1 | 32 | 63 | 164 |
| Visual Basic | 1 | 29 | 0 | 122 |
| SUM: | 871 | 24581 | 23008 | 168498 |

Phom: Persistent Homology in R
| phom 1.0.3 | |
|---|---|
| Authors: | Andrew Tausz |
| Started: | 2011 |
| Updated: | February 2014 |
| Language | files | blank | comment | code |
|---|---|---|---|---|
| C/C++ Header | 21 | 425 | 192 | 1675 |
| C++ | 1 | 47 | 19 | 176 |
| R | 2 | 59 | 45 | 118 |
| SUM: | 24 | 531 | 256 | 1969 |
Mapper
| Mapper | |
|---|---|
| Authors: | Gurjeet Singh |
| Started: | 2007 |
| Updated: | 2009 |
| Language | files | blank | comment | code |
|---|---|---|---|---|
| MATLAB | 6 | 56 | 215 | 227 |
| HTML | 1 | 21 | 38 | 114 |
| SUM: | 7 | 77 | 253 | 341 |

Python Mapper
| Python Mapper 0.1.6 | |
|---|---|
| Authors: | Daniel Müllner Aravindakshan Babu |
| Started: | 2011 |
| Updated: | March 2014 |
| Language | files | blank | comment | code |
|---|---|---|---|---|
| Bourne Shell | 8 | 3907 | 4519 | 25464 |
| m4 | 7 | 1063 | 91 | 9850 |
| Python | 19 | 1748 | 765 | 9131 |
| C++ | 1 | 329 | 140 | 2705 |
| C/C++ Header | 1 | 104 | 84 | 466 |
| HTML | 2 | 20 | 0 | 296 |
| DOS Batch | 1 | 23 | 1 | 166 |
| make | 2 | 24 | 5 | 130 |
| SUM: | 41 | 7218 | 5605 | 48208 |
Dionysus: Persistent Homology Library
| Dionysus | |
|---|---|
| Authors: | Dmitriy Morozov |
| Started: | 2006 |
| Updated: | December 2013 |
| Language | files | blank | comment | code |
|---|---|---|---|---|
| C/C++ Header | 50 | 1162 | 692 | 4842 |
| C++ | 16 | 187 | 67 | 870 |
| Python | 17 | 73 | 48 | 265 |
| CMake | 10 | 21 | 14 | 125 |
| make | 1 | 5 | 0 | 10 |
| SUM: | 94 | 1448 | 821 | 6112 |
CTL: Computational Topology Library
| CTL | |
|---|---|
| Authors: | Ryan H. Lewis |
| Started: | August 2013 |
| Updated: | July 2014 |
| Language | files | blank | comment | code |
|---|---|---|---|---|
| C/C++ Header | 58 | 856 | 3047 | 5895 |
| C++ | 22 | 309 | 1109 | 1814 |
| CMake | 21 | 113 | 168 | 393 |
| SUM: | 101 | 1278 | 4324 | 8102 |
CHomP: Computational Homology Project
People at Rutgers are also doing things. I'm not sure exactly what, but it does involve 40,000+ lines of C/C++ code related to persistent homology.
Phom Example 1
R code:
N <- 50
x1 <- rnorm(N, mean=0, sd=1)
y1 <- rnorm(N, mean=0, sd=1)
z1 <- rnorm(N, mean=0, sd=1)
x2 <- rnorm(N, mean=8, sd=1)
y2 <- rnorm(N, mean=8, sd=1)
z2 <- rnorm(N, mean=8, sd=1)
V1 <- cbind(x1, y1, z1)
V2 <- cbind(x2, y2, z2)
V <- as.matrix(rbind(V1, V2))
plot(V)
(Plotted with processing.js.)
R code:
library('phom')
#### Loading required package: Rcpp
max_f <- 9
dim <- 0
intervals <- pHom(V, dim, max_f, mode='vr', metric='euclidean')
plotBarcodeDiagram(intervals, dim, max_f, title = '')
dim <- 1
intervals <- pHom(V, dim, max_f, mode='vr', metric='euclidean')
plotBarcodeDiagram(intervals, dim, max_f, title = '')
dim <- 2
intervals <- pHom(V, dim, max_f, mode='vr', metric='euclidean')
plotBarcodeDiagram(intervals, dim, max_f, title = '')
Note that "vr" stands for the Vietoris-Rips complex.
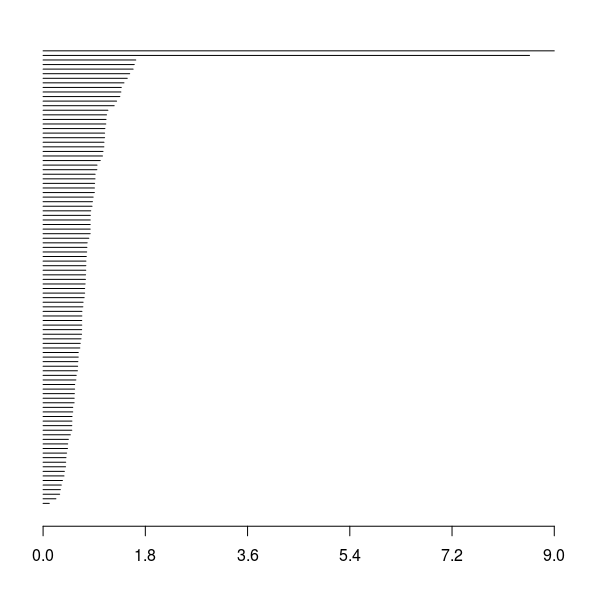
Barcode for \(\beta_0\)
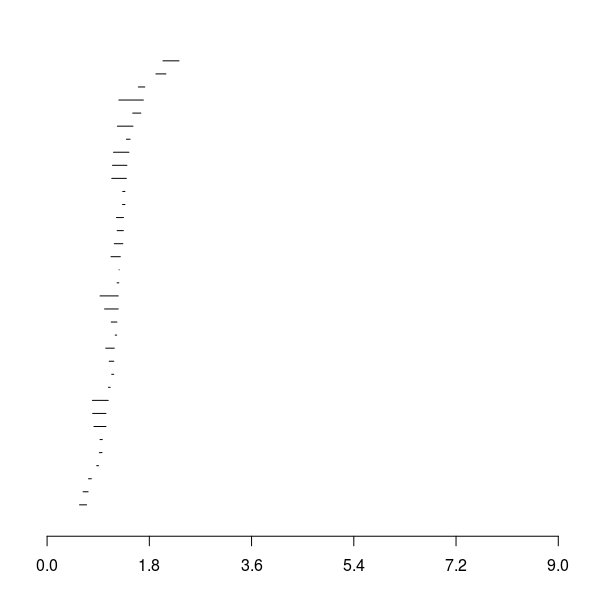
Barcode for \(\beta_1\)
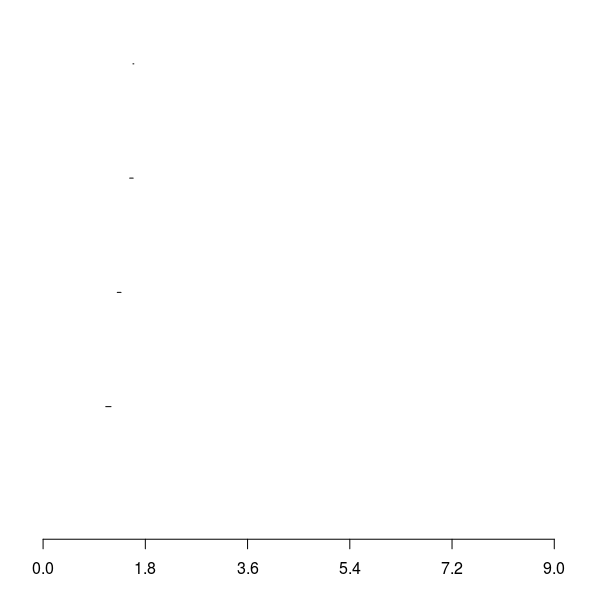
Barcode for \(\beta_2\)
Mapper does partial clustering to collapse data along a filter function and produce a simplicial complex.
Mapper Complex
The “Mapper complex” is the nerve of all partial clusters taken on the preimages of a covering of the range of a filter function \(f : S \to Z\).
where \(\mathcal{A}\) is a cover of the range of \(f : S \to Z\), \(\text{Clust} : \mathcal{P}(S) \to \mathcal{P}(\mathcal{P}(S))\) is a clustering function, and
$$P = \bigcup_{U \in \mathcal{A}} \text{Clust}\big(f^{-1}(U)\big).$$
A Circle
Matlab:
X = randn(300, 2);
X = X./(sqrt(sum(X.*X,2))*ones(1, 2));
d = L2_distance(X',X',1);
filter = d(1, :);
scatter(X(:,1),X(:,2),1000,filter,'.');
axis equal;
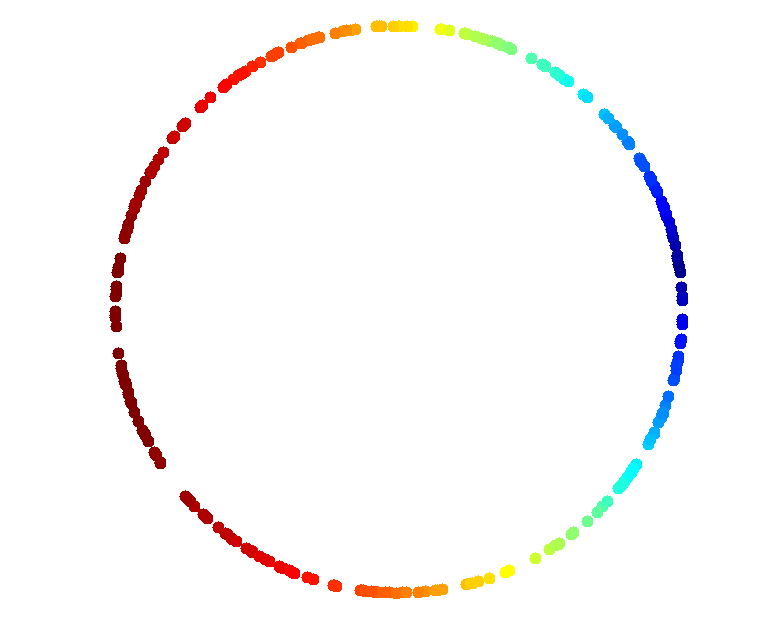
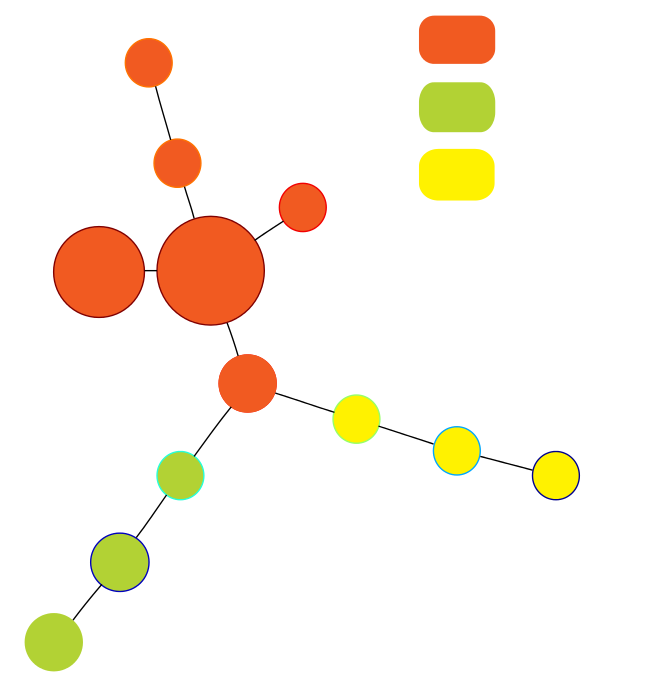
Mapper Results
Matlab:
filterSamples = 5;
overlapPct = 40;
[adja, nodeInfo, levelIdx] = mapper(d,...
filter, 1/filterSamples, overlapPct);
%%%%
for i=1:length(nodeInfo)
ecc(i) = nodeInfo{i}.filter;
setSize(i) = length(nodeInfo{i}.set);
end
writeDotFile('circle.dot', adja, ecc, setSize);
Bash:
$ neato -Tpng circle.dot -o mapper-output.png
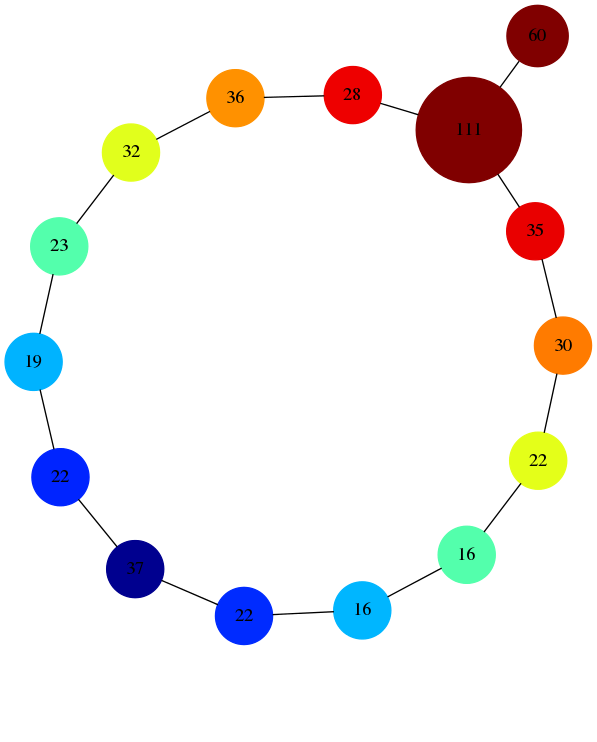
Mapper Results in the Browser
writeJsonFile('circle.json', adja, ecc, setSize);
D3.js in Python Mapper
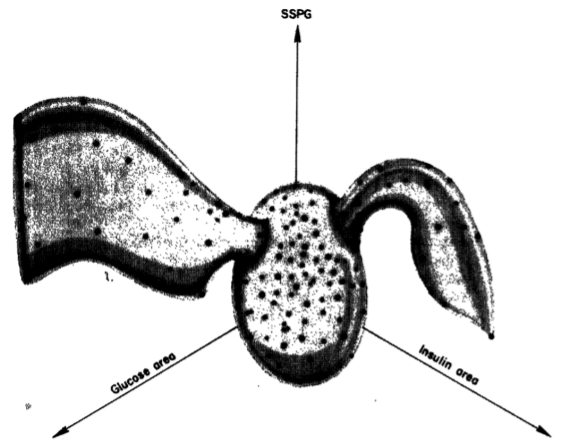
Miller-Reaven Diabetes Dataset
Reproduced Results Reproduced
R code:
require(locfit)
#### Loading required package: locfit
#### locfit 1.5-9.1 2013-03-22
data("chemdiab")
normdiab <- rbind(chemdiab)
for (i in 1:5) {
normdiab[i] <- scale(chemdiab[i],center=FALSE)
}
write.csv(normdiab,'diab-norm.csv',row.names=FALSE)
Diabetes Flares
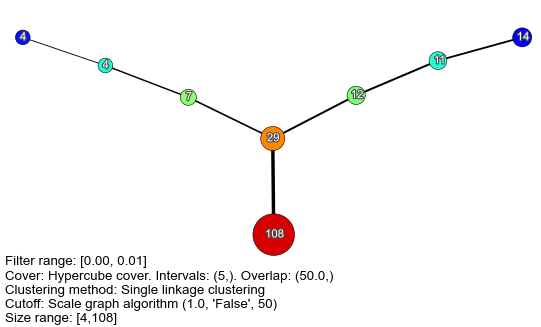
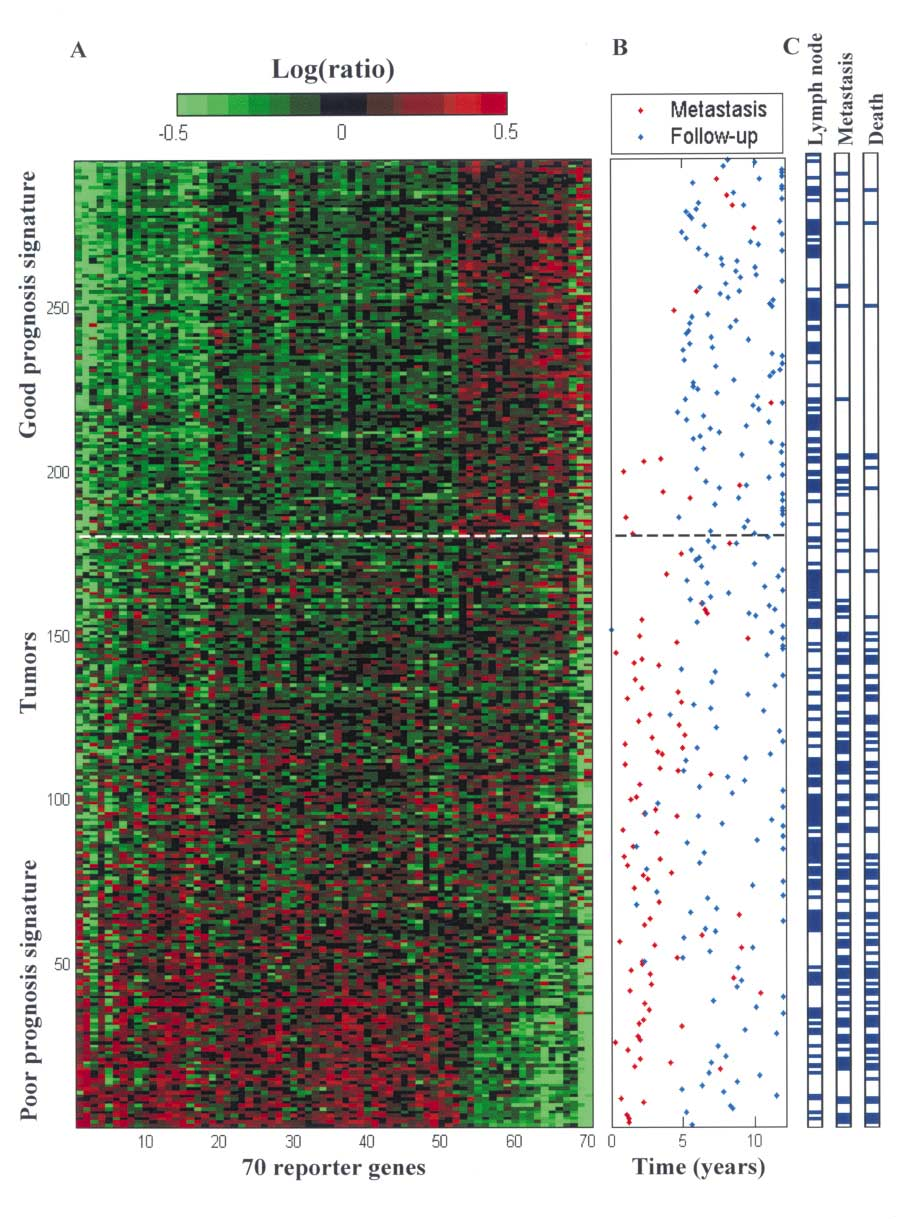
Breast Cancer
Microarray Data

Agilent Microarray
PAD = DSGA + Mapper
Progression Analysis of Disease is the one-two punch of Disease-Specific Genomic Analysis and Mapper.
DSGA = HSM + FLAT
DSGA is the one-two punch of decomposing disease data with a Healthy State Model created from normal tissue data and the FLAT construction.

Flat = data desparsing + PCA
Flat is the one-two punch of data desparsing and Principal Component Analysis.
NKI Breast Cancer Data
Normal Breast Tissue Data
UNC Microarray Database(my source)
Stanford Microarray Database(the paper's source)
Trying PAD
I replaced empty cells with NaN, deleted some poorly formatted rows, and used Matlab to impute missing data and change from log10 scale to log2 scale.
Matlab:
normal_bt = csvread('normal-breast-tissue-data.csv');
normal_bt_imputed = knnimpute(normal_bt, 10);
csvwrite('normal-breast-tissue-imputed.csv', normal_bt_imputed);
nki_data = csvread('nki-chang-complete-data.csv');
nki_data_imputed = knnimpute(nki_data, 10);
nki_data_imputed_log2 = nki_data_imputed .* 3.32192809489;
csvwrite('nki-chang-complete-imputed-log2.csv', nki_data_imputed_log2);
Online PAD Tool
c-MYB+ Cancer?
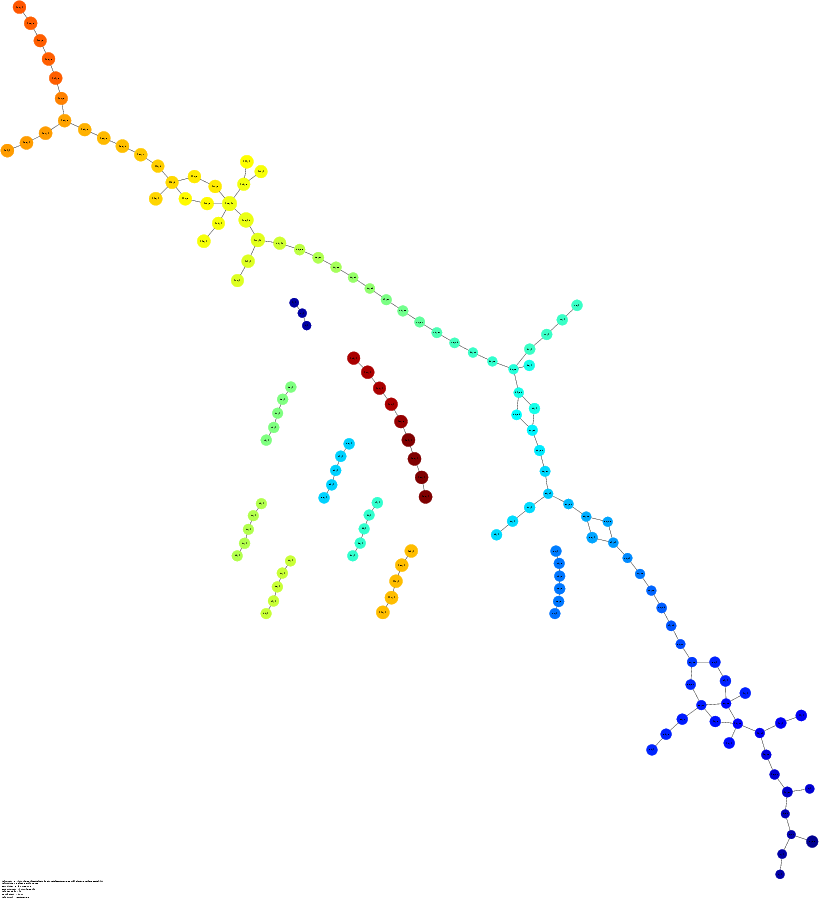
Ayasdi
References
- A. Tausz, phom: Persistent Homology in R, Version 1.0.1, 2011. Available at CRAN http://cran.r-project.org.
- G. Carlsson. Topology and Data. Bull. Amer. Math. Soc., 46:255-308, 2009.
- H. Edelsbrunner, J. L. Harer, Computational Topology: An Introduction, AMS 2010
- N. De Jong, A Probabilistic Approach To Simplicial Homology, UTK, 2012
- A. J. Zomorodian, Topology for Computing, 2005
- ...
Thank you to everybody who came out to support me, especially my committee:
Dr. Fernando Schwartz
Dr. Michael Langston
Dr. Michael Berry