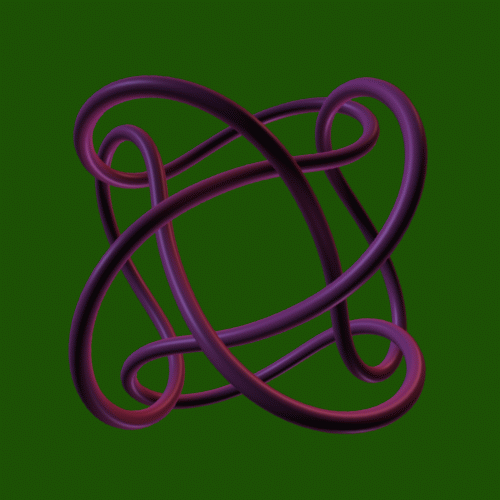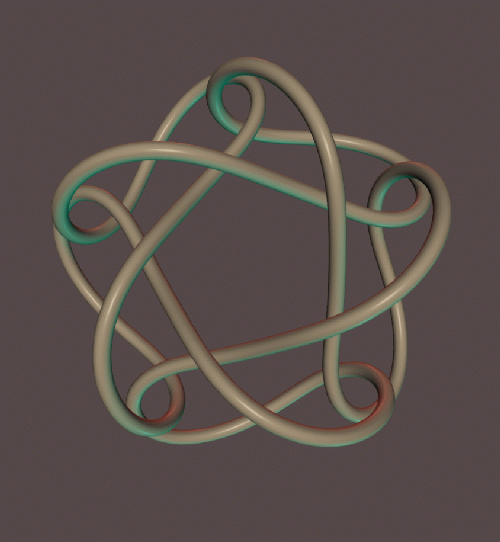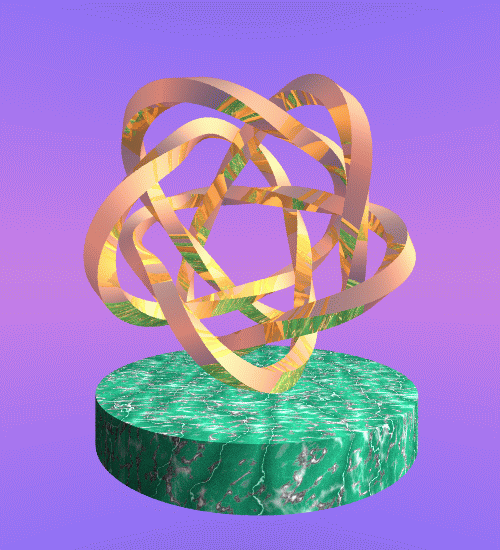A selection of symmetric knots: groups
of order up to 10
The symmetry groups of these knots were computed by
Jeff Weeks's program SnapPea,
using the canonical triangulation of the knot complement. The pictures
were produced with the help of Geomview, and
the minimal energy configurations were obtained with Ken Brakke's
Evolver, using in particular energy methods created by
Greg Buck . All these programs are
obtainable from the Geometry Center .
Rendering was accomplished using Larry Gritz's
Blue Moon Rendering Tools , with the exception of stonegold.png and
d53.png,
which were rendered using Povray.
Click on image for full-size version. To avoid dithering effects,
please view with a display allowing at least 32768 colors.
The first three knots are visibly related: they form the first three
members of a family.
 d3.png
This knot has 6 symmetries, comprising the group D3.
d3.png
This knot has 6 symmetries, comprising the group D3.
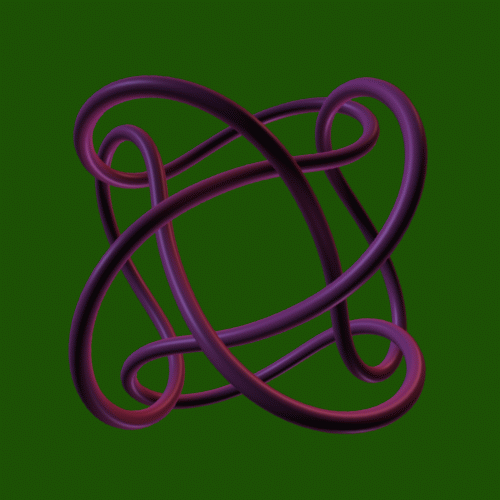 d4.png
This knot has symmetry group D4.
d4.png
This knot has symmetry group D4.
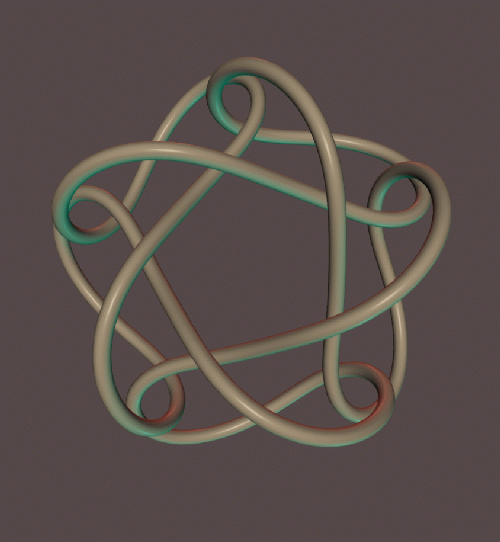 d52.png
This knot has symmetry group D5.
d52.png
This knot has symmetry group D5.
 d51.png
This knot also has symmetry group D5. The symmetries of
order 5 are fixed-point-free, and therefore are not rotations about an axis as
in the other examples. One way of "seeing" the symmetries is to notice that
the knot is the closure of the
3-string braid (s2-1s1)5.t,
where s1, s2 are standard braid
generators and t is a full twist.
d51.png
This knot also has symmetry group D5. The symmetries of
order 5 are fixed-point-free, and therefore are not rotations about an axis as
in the other examples. One way of "seeing" the symmetries is to notice that
the knot is the closure of the
3-string braid (s2-1s1)5.t,
where s1, s2 are standard braid
generators and t is a full twist.
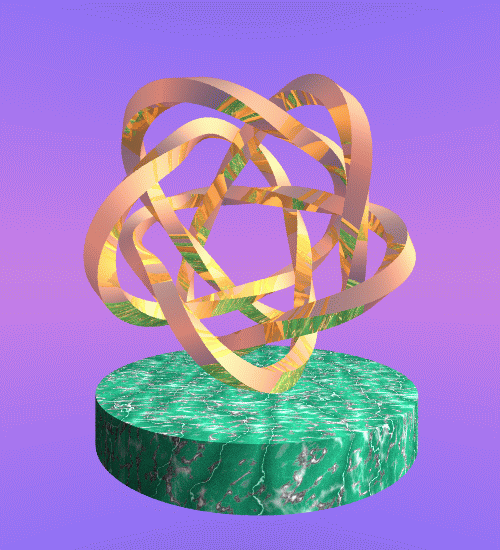 stonegold.png
stonegold.png
 d53.png
Yet another knot with symmetry group D5.
d53.png
Yet another knot with symmetry group D5.