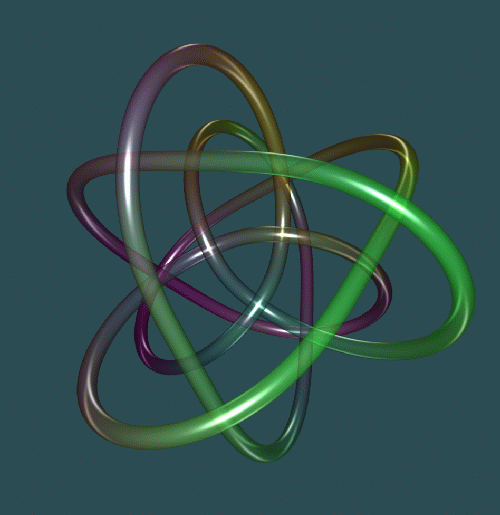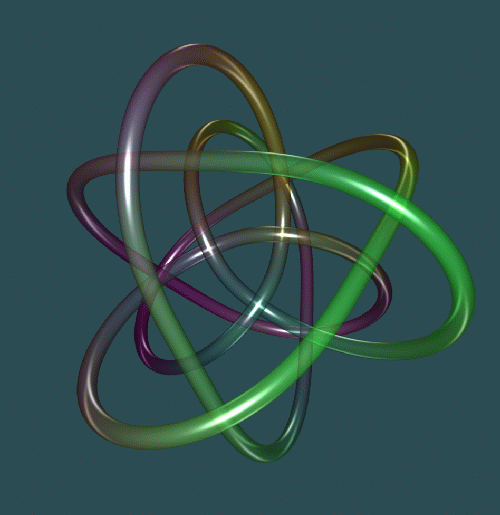The symmetry groups of these knots were computed by Jeff Weeks's program SnapPea, using the canonical triangulation of the knot complement. The pictures were produced with the help of Geomview, and the minimal energy configurations were obtained with Ken Brakke's Evolver, using in particular energy methods created by Greg Buck . All these programs are obtainable from the Geometry Center . Rendering was accomplished using Larry Gritz's Blue Moon Rendering Tools .

Click on image for full-size version. To avoid dithering effects, please view with a display allowing at least 32768 colors.

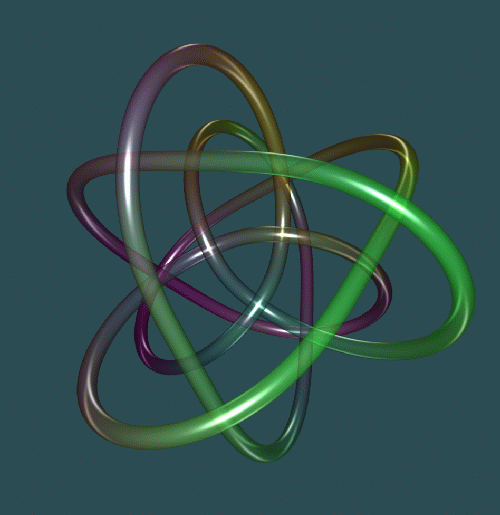d9glass.png

d9orbital.png

Two views of the 16-crossing hyperbolic knot with symmetry group D₉. A rotational symmetry of order three is clearly visible in this picture; a symmetry of order nine can also be seen, by looking at the three concentric equilateral triangles and observing how they are connected.

The previous two pictures present the D₉ knot as a closed 5-string braid. A closer inspection of this braid reveals that it can be constructed by glueing nine identical "building blocks" together. The next pictures illustrate this building block, and the method for glueing the pieces together.

d9piece2.png

Two building blocks glued together: one piece is rotated through a third of a turn in relation to the other piece.

d9space.png

Nine building blocks joined together to form the D₉ knot.