Click on image for full-size version.
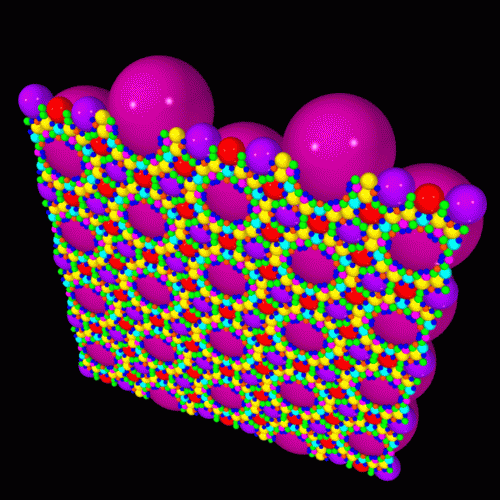
The horoball packing for the figure-eight knot, viewed from beneath upper-half space. The spheres illustrated are all tangent to the plane z=0; the spheres which are largest in the Euclidean sense have diameter 1. There are horoballs of arbitrarily small Euclidean diameter, but here a "cut-off" diameter of 0.05 has been chosen. There is one additional horoball (not illustrated), namely the plane z=1. The knot group acts transitively on the entire collection of horoballs, but there is a (parabolic) subgroup, isomorphic to Z+Z, which preserves the "infinite" horoball z=1, and which acts on the remaining horoballs via Euclidean translations. Thus the 2-dimensional pattern in this picture is repeated infinitely over the plane z=0. In general, the directions of the translations corresponding to the meridian and longitude generators of this subgroup aren't perpendicular, although they must be for amphicheiral knots such as the figure-eight. We can take a fundamental region for the Z+Z action to be a rectangle whose vertices are the points of tangency with z=0 of two adjacent full-size (pink-maroon) spheres on the left edge of the picture, together with the points of tangency of two adjacent full-size spheres on the right edge of the picture. Note that pattern of spheres has additional translational and reflectional symmetries; these correspond to the symmetries of the figure-eight knot.
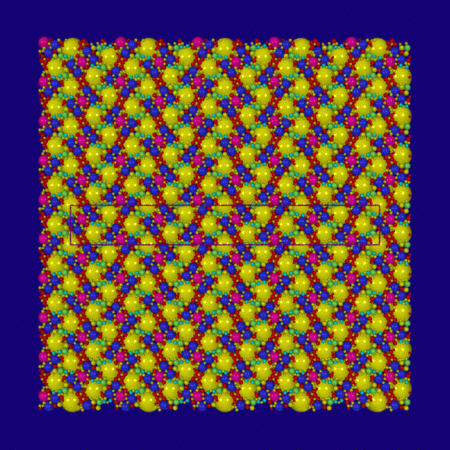
The horoball packing for the Turk's head knot. The horoballs included here have Euclidean diameters in the range from 1 down to 0.1. This 8-crossing alternating knot has symmetry group D8. The rectangle in the picture indicates a fundamental region with respect to the action of the group Z+Z of covering translations which preserve the plane z = 1. The long horizontal sides correspond to the longitudinal translation, and the short vertical sides correspond to the meridional translation. The symmetries of the knot lift to symmetries of the horoball packing, which are quite easy to spot in this example: for example, the order 8 symmetry lifts to a glide reflection along a horizontal axis.

A close-up view of the same horoball packing.
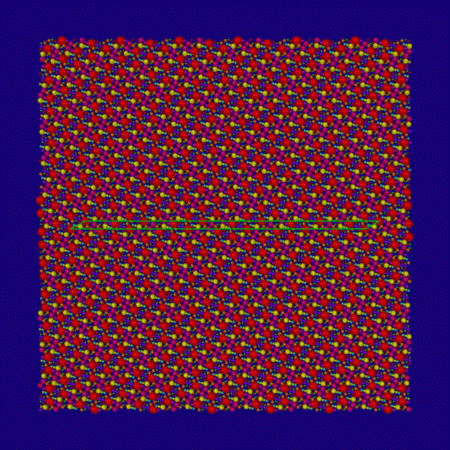
A view of the horoball packing for a 15-crossing knot with symmetry group D5. The cut-off diameter chosen in this picture was 0.1. This time, the fundamental region is not rectangular, in accordance with the non-amphicheiral nature of this knot.

A close-up view of the previous horoball diagram.