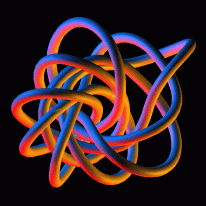local copy of www.math.princeton.edu/~debauchies/patterns/ which has disappeared...
Mathematics - The Science of Patterns and Algorithms
The mathematical sciences identify and study structures; they formulate
powerful concepts that can unify and clarify phenomena in the natural
and technological worlds, in the other sciences as well as within mathematics* itself;
they organize and design efficient ways to compute; they form the very language of
science.The start of the 21st century is a particularly exciting time.
The mathematical sciences are faced with several new challenges due to the
ever increasing demand for new mathematical conceptualization from biology and
the other experimental sciences, the pressing new challenges posed by large scale
computing and massive data sets, the many recent successes in fundamental as well
as interdisciplinary mathematics, and the promise of even more
as we confront the challenges ahead. Mathematical scientists are poised to make
significant strides, to produce new structures, and to contribute to a galaxy of new
problems, many of immediate importance to society.
------
( * Occasional use of the term "mathematics" in this text should be understood as
referring to all
the mathematical sciences; similarly "the sciences" stands as a shorthand for the
wider class of all
the pure and applied sciences as well as
engineering.)
MATHEMATICS IS POWERFUL AND EXCITING
|
picture by Robert G. Scharein
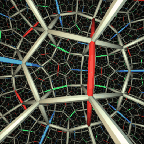
picture by C. Gunn
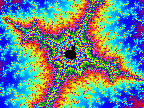
picture by Glenn Elert

picture by Glenn Elert

picture by Paul Carlson
picture by Robert Krasny
Please click on the pictures to get a larger view.
|
The Hubble telescope provided new vistas for astronomers, with mankind
sharing their excitement. Similarly, the mathematical sciences probe a
beautiful, hidden universe to be explored by all. Every subfield
can list several examples of wonderfully beautiful constructions that
delight professional mathematicians and the public at large alike; think,
for example, of Fermat's last theorem, knots, non-Euclidean geometry and
chaos and fractals. And the adventure of mathematics continues
to attract new generations of mathematical scientists.
The concepts and structures developed by fundamental mathematics often
provide just the right framework for the formulation and study of applications
in seemingly unrelated areas. Examples abound for this link from fundamental
mathematics to applied and often interdisciplinary areas. Let us just
name the importance of Hilbert spaces and Lie groups as the framework
for quantum mechanics, the foundational work in logic and combinatorics
as the basis for models of computation and the celebrated P versus NP
problem, the use of fractals for many models of natural structures, the
role played by knot theory in DNA enzymology, the geometrical framework
essential for relativity theory, and the once surprising but now ubiquitous
role of number theory in public key cryptography. Conversely, studies
of particular applications and attempts to understand the world around
us lead to abstract formulations and the definitions of new concepts,
which enrich the science of fundamental mathematics, and indeed can sometimes create
whole new fields. This mechanism gave us, for example, probability
theory, developed from observations of the variability of everyday experiences; Fourier
analysis, born from the use of trigonometric series to study the propagation
of heat; the calculus of variations, rooted in mechanics and optimization;
and differential equations, first proposed by Newton to describe mechanics and
now used in virtually all the sciences;
all giving rise to rich mathematics that provides powerful tools
for the description of an extraordinary range of phenomena. More recently,
the pursuit of efficient telecommunications drove the development of information
theory, and the experimental observation of some types of wave propagation
together with numerical experimentation led to solitons and nonlinear
integrable systems. This interaction is most often two-way. Solitons,
after their emergence from computational experiment, were soon adopted
and pursued as an interesting but purely mathematical concept, with no
thought of applications; they are now proposed for efficient signal transmission
through optical fiber cables. Other examples include harmonic analysis
and wavelet applications, each providing feedback to the other; and string
theory, a customer for topology as well as a powerful engine driving new
developments in algebraic topology. In all these links between applications
and fundamental mathematics, special excitement is generated by surprising
linkages. This excitement is also present when unexpected connections
come up between subfields within fundamental mathematics, such as the
link between knots and algebra, or the links between logic and geometry,
algebra and number theory. These are literally breakthroughs, breaching
the walls between disciplines. Such sparks can generate whole new subfields,
and they renew our constant wonder as we cross new terrain in the mathematical
world.
The science of mathematics,
providing conceptual frameworks and a common language, is
a powerful tool of insight, as well as a unifying force between all the sciences.
Mathematical abstraction and language will be essential to identify the
structures needed to organize the large volumes of data in emerging fields,
to derive new implications and new predictions to be tested. We need sophisticated
mathematical models and algorithms to make the link from measurable quantities
to the structures we want to study. Mathematics played a crucial role
in generating and assembling the fragments of the human genome. Completion
of the sequencing of the genome has revolutionized biology, and will revolutionize
many other areas of science. Translating the genome into knowledge about
the function of genes requires extensive mathematical modeling. The mathematical
sciences will play a significant role in understanding the complexities
of life processes, and improving human health. On the other hand, new
understanding of life processes may lead to new algorithms and new modes
of computing.
The mathematical sciences also serve as a vehicle for scientific
cross-fertilization, when
ideas from one area, abstracted and formalized by mathematicians, turn
out to be essential in other areas. Dynamical system ideas, distilled
from mechanics, find rich applications in ecology; approaches to the partial
differential equations of fluid dynamics provide useful tools in image
analysis; the wavelets/harmonic analysis synthesis was the bridge over
which sub-band filtering, developed by electrical engineers, jumped to
applications in medical data processing, and computational physics and
chemistry [DA]; coding theory, developed to transmit and store information
reliably in the error-prone world of communications and computers, later
found applications in many other fields, including biology; statistical
ideas, developed in connection with problems in the social sciences and
agriculture, now permeate disparate fields, from genomics to finance.
|



picture by S. Gunturk and I. Daubechies
CHALLENGES AND OPPORTUNITIES FOR MATHEMATICS
Models and Simulations
Simulation and computing have become an essential part of modern science
and engineering, complementing theory and experimentation. This development, driven by
access to ever more powerful computers, poses new challenges to the
mathematical sciences.
At the heart of any simulation is a model, a mathematical formulation
that captures the structure and form of real-world phenomena. This model
is typically surrounded
by numerical techniques that produce quantitative information sometimes
augmented by estimates of reliability, and by computer visualization that allows
results to be manipulated and summarized, leading to qualitative understanding
that inspires further analysis. Each of these elements requires sophisticated
mathematics.
In modeling complex and poorly understood phenomena, such as weather or
the stock market, the modeler encounters data that are uncertain, inaccurate,
inconsistent, incomplete, and/or insufficient to determine a solution. [MS]
For example, numerous medical conditions produce very similar CAT scan
images, yet doctors must decide on the most plausible diagnosis.
Typically, the input data, the modeling process
and the solution may contain random
and systematic errors and thus need statistical and/or probablistic analysis.
On the other hand, solving a problem exactly may
be computationally intractable; finding approximate solutions that have sufficient accuracy
is then another challenging task, requiring a careful mathematical analysis.
The resultant
uncertainty assessment provides a mechanism to drive confidence in the validity of
the computed solution [GL]. For the
simplest cases in which phenomena are nearly linear, powerful mathematical
and computational tools have been developed over the last 50 years to estimate and deal
with these various forms of uncertainty. Genuinely nonlinear problems,
however, are still far
beyond reach [MS].
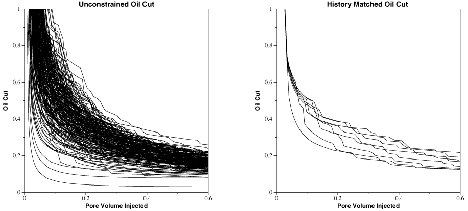 picture by J.Glimm
picture by J.Glimm
A particular challenge is posed by "model reduction".
Technology relies increasingly on models that describe
huge systems on fine scales in length and time while data and conclusions
may be concentrated at coarser scales only. Unwieldy fine-scale equations
need to be replaced with effective coarse-scale descriptions in order to
provide more accurate predictions when computation and analysis on the fine
scale is totally unfeasible. Stochastic modeling can also be used to
provide a huge reduction
in complexity. The challenge to the mathematical sciences is to
develop systematic approaches to bridge these levels of organization.
Important examples include global climate change, environmental remediation,
computer-assisted design for manufactured products, neuroscience, and
chemical kinetics of drug design [GL]. Similar organization and reduction are
needed in settings where the multiple scales do not result from
physical scaling in time or length, but are discrete or hierarchical,
such as in multilayered descriptions of large
networks [MS].
In many of these areas, we have made progress in the past, but we
still need many orders of magnitude improvement before we can tackle truly realistic
problems. These activities require substantial effort in collaboration
between mathematical and other scientists as well as novel mathematical insight
to create new techniques that allow qualitative insights needed to make further
breakthroughs.
Computing with Large Data Sets
Breakthroughs in sensor technology are leading to generation of unprecedented
volumes of high-dimensional data. The amazing continued growth in
the raw power of computers and algorithmic advances offer the promise of
addressing the tremendous challenges of analyzing such data. Huge data sets,
terabytes of data, in very high dimensional spaces, are now collected
routinely in almost all sciences [MS]. Examples are images from diverse sources,
dynamics of the internet, neural recordings and, in the discrete domain,
gene expression arrays. Whereas data sets in 1,2 or 3 dimensions are
easily visualized and analyzed, data sets in 1000 dimensions are much harder
to understand. Even 10,000 points constitute a very sparse set in 1000-dimensional
space and it is easy to "overfit" the data with a model that makes
you detect spurious "patterns" that disappear when you acquire more data.
A major challenge is to find methods to analyze the structure of such
sets, to fit models robustly and identify and validate patterns. Techniques
from statistics, harmonic analysis, graph theory and computer science are only
beginning to clarify this problem.
Geometrization of Topology and Physics
The interaction between geometry, topology, physics, and cosmology
continues to enrich all these disciplines despite (or perhaps because
of) their apparently different goals.
One current area of excitement
is "mirror symmetry," which relates certain six-dimensional manifolds
that arise in string-theoretic physics to each other [TA]. The spaces in question
are not new -- their structure and properties were explored by
differential geometers some years ago, and this work was essential for
the new developments in string theory. However the notion of mirror symmetry
is new -- it was revealed by the use of these spaces in physics.
Now the task of understanding mirror symmetry is leading to entirely new
mathematics. Efforts to determine the origin of this symmetry, its
intrinsic structure, its implications, and especially its generalizations
are leading to fundamental questions such as: counting
the solutions of certain polynomial and differential equations;
exploring certain relations between symmetries of the circle,
of matrices, and of higher-dimensional manifolds;
and exploiting a new correspondence between solutions of certain equations
involving few parameters and solutions of other equations involving
many parameters.
Another currently exciting area is the
study of four-dimensional manifolds [ST, TA]. Here mathematicians
have constructed inexorably complicated families of four-dimensional
manifolds that are distinguished by invariants derived from the study
of the relationship between gravity and the other physical forces.
We have only a small glimpse of the richness of four-dimensional
manifolds. As this interplay deepens new mathematics and physics will
be developed.
Noise
Noise and randomness are ubiquitous. The correspondence between random walks and
diffusion differential equations has provided fertile territory for
mathematical analysis, and for applications such as stochastic control,
filtering, and predicting the likelihood of rare but
catastrophic events. We have become adept at dealing with random perturbations
of finite dimensional systems, described by ordinary differential
equations. In contrast, the analysis of similar issues for infinite dimensional
systems (those described by partial differential equations) is in its
infancy. Learning how to deal with them is essential to
our understanding of the consequences of uncertainty,
imperfection, and thermal fluctuations in physical systems [KO,GL]. By
analogy with the existing theory, it will involve random walks in and diffusion
differential equations on infinite-dimensional spaces.
Related issues of infinite-dimensional analysis arise
in the task of putting realistic quantum field theories on a
mathematically sound foundation. Fresh insight in this area is emerging
from links between string theoretic physics, topology, and geometry.
A different mandate for infinite-dimensional analysis comes
from today's massive data sets, which must typically be interpreted using
models with large numbers of parameters. Infinite dimensional approximations
provide one approach to get a handle on the
behavior of statistical methods in the limit of increasingly large
data sets and models [BI, BO].
Most of these infinite-dimensional problems defeat us at present; gaining better
insight would have extraordinary pay-off. What we can glimpse already
has spectacular ramifications.
Nonlinearity
Understanding nonlinearity is a central challenge for modern science.
This is a huge task, since there are many sources and many sorts of nonlinearity.
Sometimes its origin is the behavior being modeled: physical
examples include combustion, phase transformation, and turbulence; biological
examples include protein folding and excitable tissues, such as heart
muscle and the nervous system. Nonlinearity can also
come from other, more structural sources such as feedback or
geometry: examples include the optimization of financial decisions;
the pinch-off of fluid droplets; and the motion of surfaces under
curvature-driven flows.
We have accumulated great insight into nonlinear phenomena,
and a rich collection of viewpoints and methods, such as asymptotic analysis,
bifurcation, chaos, shock waves, and viscosity solutions,
to name but a few. Our powerful and ever-expanding collection of tools
provides many opportunities for advancement. For example,
new methods from the calculus of variations are giving fresh insight into
the design of composites with optimal microstructures, the consequences
of polycrystalline structure in shape-memory materials, and the arrangement
of domain walls in magnetic materials [KO]. Another example: nonlinear
evolution equations adapted from geometry and fluid dynamics are being used
for the creation, manipulation, smoothing, and segmentation of visual
images [CH,MU,EV]. A third example: dynamical systems methods are providing
insight into the sources and consequences of spatio-temporal patterns,
including fibrillation of heart tissue and rhythmic electrical activity
in the nervous system [KL].
And yet our mastery of nonlinearity has barely begun. Many fundamental
questions remain open, for example: Are solutions of the Navier-Stokes for fluid mechanics
equations unique in three space dimensions? What about (viscosity) solutions
of systems of hyperbolic conservation laws? These questions are
mathematical challenges of course, but their importance goes much deeper.
They address the adequacy of our standard mathematical models for
fluid mechanics and gas dynamics. If solutions were not unique -- which
would be a big surprise -- then some effect we usually ignore would actually
be crucial for determining the physically correct solution. If, as seems
more likely, solutions are unique, then the methods developed to prove this
assertion will also give insight concerning qualitative features of
flows and the accuracy and stability of numerical solution schemes. Recent
breakthroughs on uniqueness for conservation laws makes this topic
particularly timely [EV].
Beyond Fermat
One of the most widely publicized mathematical results of the last few
years is Wiles' proof of Fermat's last theorem : that the sum of two nth
powers can not be another nth power if n>2. This had been an unsolved problem for 350
years, and that reason alone would make it of great interest. But mathematicians see
it as one result in a huge web of connected conjectures, some proven and
some supported by extensive computations which together link arithmetic, geometry,
analysis, group theory and even physics. These conjectures, and the powerful
methods that are being developed to deal with them, have been some of the
most exciting themes in fundamental mathematics in the last 50 years. Among
these is the ABC conjecture which generalizes Fermat's theorem and expresses
a fundamental tension between addition and multiplication: If A and B are any two
numbers with many repeated large prime factors, then their sum cannot have many
repeated large prime factors (here "many" can be made precise). Other conjectures
relate to the distribution of prime numbers, 2,3,5,7,11, .... This tantalizingly
irregular sequence is encoded in a kind of generating function, the Riemann zeta
function, whose analytic properties express the hidden patterns of the primes in
a way which is worked out in this complex of ideas. The Riemann zeta function
is the paradigm of a class of functions whose analytic properties are expected
to shed light on such classical Diophantine questions as: how many rational
solutions does a (given) cubic polynomial in two variables have? This vision
connects to the theory of group representations, to the theory of transcendental
numbers, and to the study and classification of polynomial equations. The study
of polynomial equations and the locus of their zeroes is nowadays being energetically
furthered by methods from physics, partial differential equations, and differential
geometry. It is even expected
that work in this area will shed light on the structure of finite simple groups
(the "Monster group" in particular).
The breadth and unity of this development is hard to exaggerate; it makes for
a particularly interesting time in number theory, with many challenges ahead.
Mathematics for Biology and Medicine
Biology and medicine are poised to climb the twin peaks of understanding
the life process and greatly improving human health. Success of these
efforts depends on the increasing involvement of the mathematical sciences.
Combinatorics and statistics have already made essential contributions to
the rapid and successful sequencing of the human genome. Obtaining the DNA
sequence is just the first step in computing the secrets of life; decoding
the meaning of the sequence poses serious long-term scientific and
mathematical challenges. We must design new methods of exploration and
analysis that combine the power and precision of both biology and
mathematics. At the cellular level, we must find both the genes which
encode for currently unknown proteins and the non-coding DNA regions which
regulate the expression of these new genes. This step will involve pattern
recognition, signal processing, database mining, statistical methods both exploratory
and confirmatory, and new biomathematical
cryptology techniques many of which have
yet to be invented. After discovering a new protein,
we must determine its function, regulation, and role in a cascade
network of interaction with other proteins. This will involve comparison of
characteristics of the unknown protein to those of known proteins, both
human and non-human. This comparison involves measurement of similarity of
DNA sequences (coding and regulatory), similarity of spatial geometry of
native folded states, similarity of regulation patterns using
microarray chips, and the establishment of cause and effect relationships
between the many actors in these processes.
New mathematical and statistical ideas are required for this step: we
need new biologically relevant similarity measures of 1D sequences, 3D
geometry, clustering algorithms and other statistical analysis methods
for expression vectors of very high
dimension. At the macroscopic level, a fundamental problem in medicine is
to define and understand ranges of parameters which correspond to "normal"
anatomy and function for an organ, a necessary first step before understanding and
treating the "abnormal" . Due to high variability, comparison of
anatomical and functional information across individuals and groups
requires new mathematical and statistical models as well as highly sophisticated
computational algorithms. A goal in medicine is to have
normal organs and organ systems "in silico", allowing non-invasive
computational comparison between subject and template, enhancing detection
of disease states and design of treatment. The mathematical sciences have played and will
continue to play an essential role in the team effort to understand the
complexities of biology and harness this understanding to improve human
health.
Information Technology
Stunning advances in information technology have not only profoundly changed
the way we live and the way we think, but also offer major challenges for the
mathematical sciences in partnership with computer science. Because the basic
structures in information technology are discrete rather than continuous, new
approaches in combinatorics, logic and statistical modeling are necessary to
cope with problems that are growing daily in complexity and size. Just as physics
was a motivating force for many mathematical fields in the past, information
technology will act as an engine driving the development of new mathematics
in the future. Much of today's computing is increasingly interactive, distributed,
and heterogeneous---properties that exacerbate the inherent difficulties of
maintaining security, privacy, and speed. Communication networks, wired and
wireless, span the globe and are being built at a dizzying pace; their ability
to function depends on understanding very large, complex graphs. Despite progress
in analyzing the efficiency, performance, and tractability of algorithms, very
little can be said about problems for which only partial information is available
or the input sizes far exceed available memory. Software is everywhere, yet
mathematical techniques for assessing, improving, and ensuring its reliability
fall far short of the needs. There is work on the table!
The consistent spectacular growth in raw computing power during the past 30
years is common knowledge. It is less widely known but equally significant that
advances in numerical algorithms have matched, and often exceeded, that pace.
Solving larger, more nonlinear, more complex problems will continue to require
smarter, more sophisticated mathematics to create new algorithms. For example,
large-scale optimization, continuous and discrete, has had a significant impact
in a wide range of areas, including manufacturing, scheduling, routing, real-time
control of physical systems, and Web caching; however, techniques for handling
the important class of nonlinear mixed integer-continuous problems are still
in their infancy in terms of analysis and algorithms.

picture from Applegate, Bixby, Chvatal and Cook
Click on picture for more detailed version
The familiar model of sequential computation has been expanded in concept
by parallel, heterogeneous, and distributed computing. But this is not the only
conceivable form of computation. The field of quantum computing, the subject
of intense recent publicity, is emerging as a rich source of mathematical inquiry into
the nature of computation and communication. From another domain, the processing
and transformation of information within biological organisms offer a rich opportunity
for new mathematical paradigms of computing. The associated mathematics would
provide a deeper understanding in biology, including the neurosciences, and
molecular- and population-level systems.
These eight paragraphs illustrate the diversity and intellectual excitement
characteristic of mathematics. They are representative of a much richer
web of mathematical challenges and accomplishments not presented here. Even
in this set of examples, linkages among topics indicate the unity and inseparability
of this research enterprise. For example, nonlinearity is a profound challenge
within simulations. Large data sets and infinite dimensional stochastic
processes are intrinsically linked and both are connected to model reduction, inverse
problems and uncertainty. Similarly connections between number theoretic questions
and the geometrization of topology and quantum physics are impressive.
The many new exciting results within mathematical discipline as well as the striking
connections between them, and the important opportunities offered by these developments and
by
the challenges to mathematics posed by the other sciences, make this an especially exciting
time for researchers in the mathematical sciences, who look forward to the adventure.