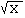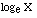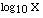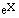4 INTRINSIC FUNCTIONS

The equation needed for the carbon dating problem is

The natural logarithm of the value of the remaining carbon 14 is needed.
The computer can be particularly useful in solving this equation since
some frequently used computations are built into the
FORTRAN language. These built in operations, such as, square root,
absolute value, and tangent, are called intrinsic functions. The
natural logarithm of X is such an intrinsic function. These functions
are accessible directly from a FORTRAN program. The argument of a
function is the input value to that function and can be a constant, a
variable, or an expression. An intrinsic function and its
argument represent a value. The type of value returned by a
function is determined by the function. Some intrinsic functions are
generic meaning that they return the same type as their input
argument. Table 1 lists some commonly used intrinsic functions. The names
of the arguments specify their type; X is REAL, IX is INTEGER, GX is an
argument of a generic function.
Table 1: Intrinsic Functions
| Name |
Value |
Comment |
| REAL(GX) |
real value of GX |
converts the argument to a real value |
| INT(GX) |
integer part of GX |
converts the argument to an integer value |
| SQRT(X) |
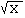 |
calculates the square root of X |
| LOG(X) |
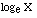 |
calculates the natural log of X (base e) |
| LOG10(X) |
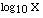 |
calculates the common log of X (base 10) |
| SIN(X) |
sine of angle X |
calculates the sine of X (X expressed in radians) |
| NINT(X) |
rounded integer value of X |
rounds X to nearest integer value |
| COS(X) |
cosine of angle X |
calculates the cosine of X (X expressed in radians |
| EXP(X) |
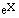 |
raises base e to the x power |
| ABS(X) |
|X| |
calculates the absolute value of X |
| MAX(GX,GY,...) |
maximum of (GX, GY, ...) |
returns the maximum value of GX, GY,... |
The REAL function can help avoid mixed mode arithmetic
expressions by
explicitly converting variable types. For example, when computing the
average of a set of REAL values it is necessary to divide the real sum of
the values by the number of values. Use the following statement to
convert the integer number of values into a real value for the division:
- aver = sum/REAL(n)
If INTEGER values were used to obtain the value of sum, the sum would
also be an INTEGER. To represent the average by a REAL value, use the
following statement:
- aver = REAL(sum)/REAL(n)
It is possible to nest intrinsic functions, that is, to use the
function of one intrinsic function as the argument for another function
(composition of functions). The following statement uses the composition
of the ABS function and the LOG function to compute the
natural logarithm of the absolute value of r
ablog = LOG(ABS(r))
Example
Program Description
This program computes and outputs cosine(x), cosine(x)^2, and the square
root of x.
Input/Output Description
The output consists of the value of x, cosine(x), cosine(x)^2, and the
square root of x.
- Algorithm
- Calculate cosine(x), cosine(x)^2, and the square root of x.
- Print the value of x, the cosine(x),cosine(x)^2, and the square root
of x.
Code
Intrinsic Functions Example Program
EXERCISES
1. Line Segment Program
Program Description
It is possible to determine the distance between two points (A and
B) and the midpoint of the two points when you know their
coordinates.
Write a FORTRAN program that determines the distance between two
points
(the length of segment AB) and the midpoint of the points.
Input/Output Description
The values for the x and y coordinates for point A and point B are
assigned.
The output is the length of segment AB and the midpoint of
segment AB.
Mathematical Equations
The length of segment AB is calculated: length = sqrt((x2-x1)**2
+ (y2-y1)**2).
The x coordinate of the midpoint of segment AB is calculated: xmidpt
= (x1 + x2)/2.
The coordinate of the midpoint of segment AB is calculated: ymidpt
= ((y1+y2)/2
- Algorithm
- Assign the x and y coordinates for point A.
- Assign the x and y coordinates for point B.
- Calculate the length of segment AB.
- Calculate the midpoint of segment AB.
- Print the length of AB and the midpoint of AB.
Code
Part of the code is done for you. Follow the steps below to
complete it.
- Key in the partially completed line segment
program.
- Add documentation (program headings, variable list, explanation
of the use of the SQRT function). Fill in values for each ???? in the
program.
- Compile and execute the program.
- Modify the program to read in three points and to calculate and
print the distance between points one and two, points two and three, and
points one and three.
2. Roller Coaster Problem
- Problem Statement
- The plans for a new roller coaster call for a portion of the track to
be built in the shape of a sinusoid. The high
and
low points on the track are separated by 50 m horizontally and by 30 m
vertically. The low point is 3 m below the ground. The vertical
timbers are spaced every 2 m. The track first goes below ground at
39.76 m from the high point of the track. Calculate the length of the
vertical support at any point from the high point of the track.
- Input/Output Description
- The output is the length of the vertical support and the distance of
the support from the high point of the track.
- Mathematical Equation
-
- The general equation of a sinusoidal function is
y = C + A cos B(x-d) where
A, B, C, and D are constants.
Let y be the
number of meters the track is above ground and x the number of meters
horizontally from the high point. The equation for this problem expresses
the length of the vertical supports in terms of x.
The equation for the length of the vertical supports is
length = 12 + 15 * COS(3.14159/50 * x)
- Algorithm
- Calculate the length of the vertical support.
- Print the length.
Execute the program with each of the following x values and complete the
chart.
| X |
Length |
X |
Length |
X |
Length |
X |
Length
| X |
Length |
| 2 |
|
10 |
|
18 |
|
26 |
|
34 |
|
| 4 |
|
12 |
|
20 |
|
28 |
|
36 |
|
| 6 |
|
14 |
|
22 |
|
30 |
|
38 |
|
| 8 |
|
16 |
|
24 |
|
32 |
|
40 |
|
What do the negative values represent?
3. Carbon Dating Problem
- Problem Statement
Carbon dating is a method for estimating the age of organic substances.
It compares the amount of carbon 14 contained in the remains of the substance
with the amount of carbon 14 that would have been in the object's
environment at the time it was alive. Write a program that reads the
proportion of carbon 14 remaining in an artifact and then calculate
and print the estimated age of the artifact.
- Input/Output Description
- The input is the proportion of carbon left in the artifact.
The output is an estimate, in years, of the age of the artifact.
- Mathematical Equation
The following equation gives the estimated age in years of an artifact
using the LOG function (base e).
age = -(LOG(carbon)/1.216 E-0.4)
where
age = the age of the substance
carbon = the carbon 14 proportion remaining in the substance
Algorithm
- Input the proportion of carbon 14 remaining in the artifact.
- Calculate and print the age of the artifact.
4. Population Growth Program
Problem Statement
A geometric growth model can be used to determine the change in
population. If the growth rate is positive then the population
will
increase, but if it is negative, the population will
decrease.
Write a FORTRAN program that calculates the population growth of
an area.
Input/Output Description
The user inputs the values for the present population size, the
number of years, and the annual difference between the birth rate
and death rate.
The output is the change in the population.
Mathematical Equation
The growth model formula is:
 where:
where:
- p = present population size
- m = number of years
- r = annual difference between the birthrate and death rate
-
Algorithm
- Read the current population.
- Read the number of years.
- Read the annual difference between the birthrate and death rate.
- Compute the change in population.
- Print the change in population.