Adaptive TraceFEM

Stabilized scheme for surface heat equation

The paper introduces an adaptive version of the stabilized Trace Finite Element Method (TraceFEM) designed to solve low-regularity elliptic problems on level-set surfaces using a shape-regular bulk mesh in the embedding space. Two stabilization variants, gradient-jump face and normal-gradient volume, are considered for continuous trace spaces of the first and second degrees, based on the polynomial families $Q_1$ and $Q_2$. We propose a practical error indicator that estimates the ‘jumps’ of finite element solu- tion derivatives across background mesh faces and it avoids integration of any quantities along implicitly defined curvilinear edges of the discrete surface elements.

read

Q-tensor hydrodynamics on films

Evolution of defects and the 3D escape

We develop a Q-tensor model of nematic liquid crystals occupying a surface which represents a fixed fluidic material film in space. In addition to the evolution due to Landau– de Gennes energy the model includes a tangent viscous flow along the surface. The coupling of a two-dimensional flow and a three-dimensional Q-tensor dynamics is derived from the generalized Onsager principle following the Beris–Edwards system known in the flat case. The main novelty of the model is that it allows for a flow of an arbitrarily oriented liquid crystal so the Q-tensor is not anchored to the tangent plane of the surface. Several numerical experiments explore kinematical and dynamical properties of the novel model.

read

Harmonic map flows

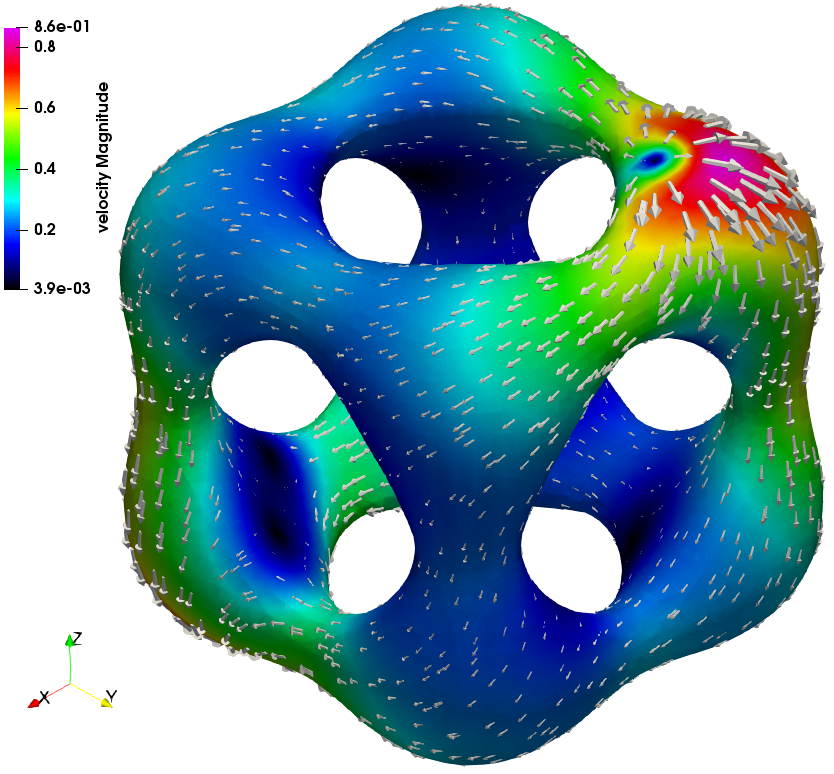
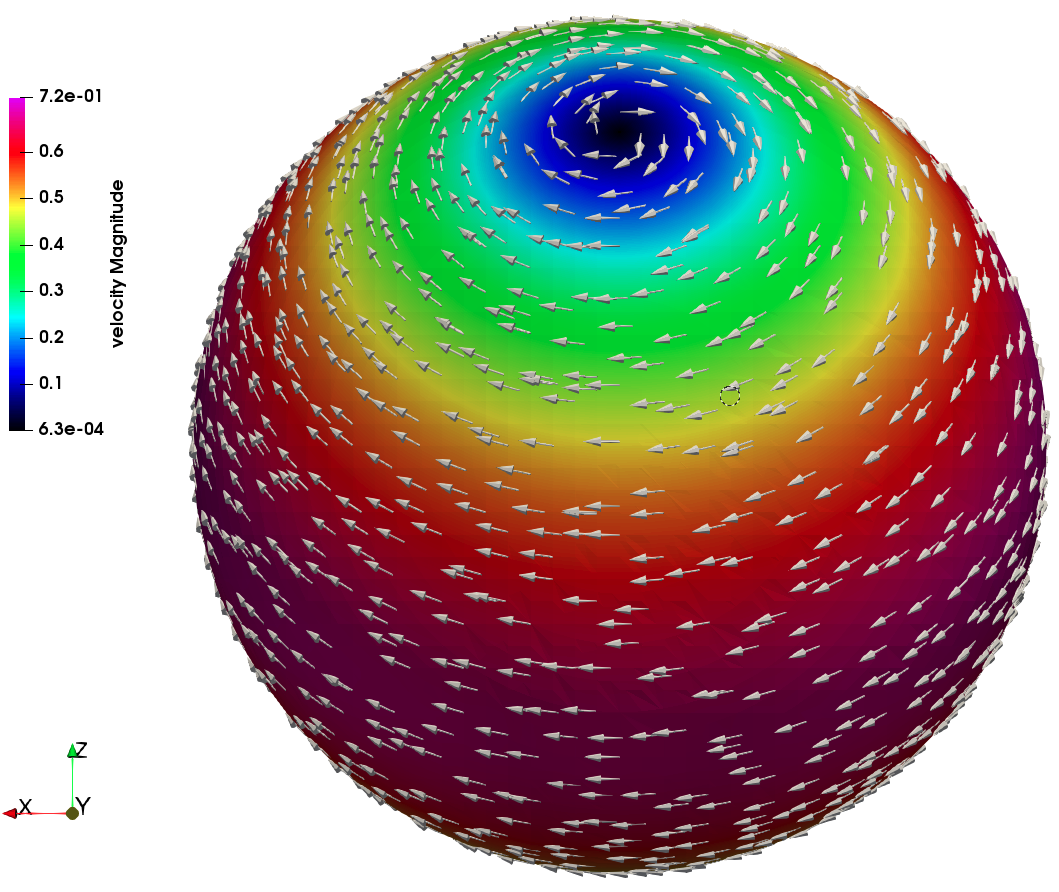
Minimization of Frank's energy in unfitted domains

Harmonic map flows are closely related to the minimization of Dirichlet energy $E$ among the maps between two Riemannian manifolds. Consider the set of maps $\mathbf{n}$ from a domain $\Omega{} \in \mathbb{R}^3$ to the unit sphere $S^2$ embedded in Eucledian space, \begin{equation}W^{1,2}(\Omega{}, S^2):=\{\mathbf{n} \in W^{1,2}(\Omega, \mathbb{R}^3): \quad{}\mathbf{n}\in S^2 \text{ a.e. in }\Omega\}\,, \end{equation} elements of which have finite Dirichlet energy $E_F[\mathbf{n}]=\frac{1}{2} \|\nabla \mathbf{n}\|_\Omega^2$. 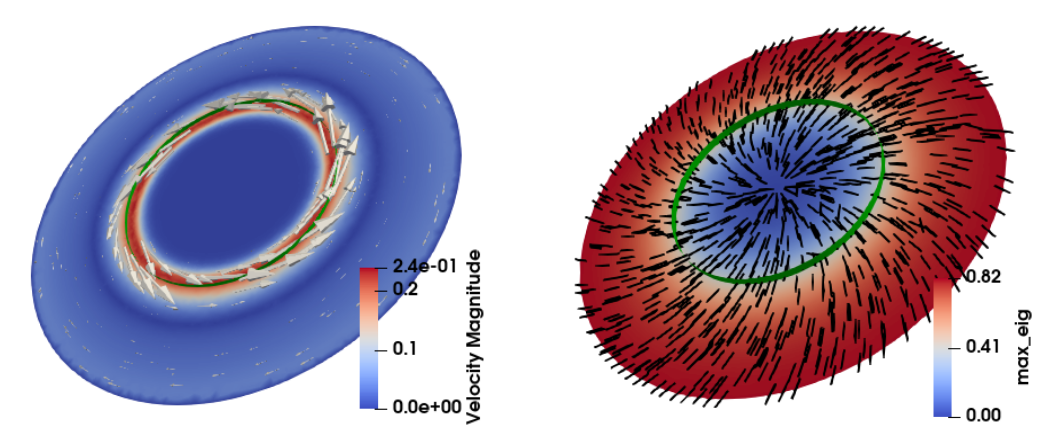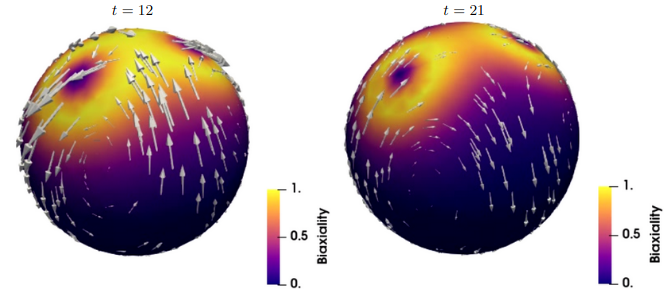This constrained energy corresponds to the Oseen-Frank model of liquid crystals. Computation of a minimizer $\mathbf{n}^*$ of $E_F$ is a very challenging task. First, the construction of discrete spaces of maps with values in $S^2$ is not trivial, e.g. polynomial interpolation violates the unit-length constraint. Another issue is that the Euler-Lagrange equation is nonlinear \begin{align} \label{system1}\Delta\mathbf{n}^*+|\nabla{}\mathbf{n}^*|^2\mathbf{n}^*&=0\text{ on }\Omega\,, \qquad{} \mathbf{n}^*(x)\in S^2 \text{ on }\Omega\\ \label{system2}\mathbf{n}^*&=\mathbf{g}\text{ on }\Gamma\,, \qquad{} \partial_\nu{}\mathbf{n}^*=0 \text{ on }\partial\Omega{}/\Gamma \end{align} Instead of the finding solutions of Euler-Lagrange equation, it is suggested to solve a constrained evolution equation for the time-dependent map $\mathbf{n}(t)$ and Lagrange-multiplier $\lambda(t)$ of the unit-length constraint: given the initial guess $\mathbf{n}^{0}$ , we conduct a constrained *-gradient flow $(\mathbf{n}(t), \lambda(t))\in H_\mathbf{g}\times L^2(\Omega)$ on $[0,T]$ with respect to the metric induced by a $\|\cdot\|_*$ norm in order to arrive at an approximation of the minimizer $\mathbf{n}^*$: \begin{align} (\mathbf{n}_t(t), \mathbf{m})_*&=-\left<\partial_{\mathbf{n}}L_{\mathbf{g}}[{\mathbf{n}(t)},{\lambda(t)}],\mathbf{m}\right>\\ 0&=\left<\partial_{\lambda}L_{\mathbf{g}}[{\mathbf{n}(t)},{\lambda(t)}],\mu\right>\, \end{align} for all $(\mathbf{m},\mu) \in H_0 \times W^{-1,2}(\Omega{})$, where the Lagrangian is penalised to enforce the Dirichlet boundary condition: \begin{equation} {L}_{\mathbf{g}}[\mathbf{n},\lambda]=\int_{\Omega}\frac{1}{2}|\nabla\mathbf{n}|^2+\int_{\Omega}\frac{\lambda}{2}(\mathbf{n}\cdot\mathbf{n}-1)+\int_{\Gamma}\frac{1}{2\epsilon}(\mathbf{g}-\mathbf{n})^2, \end{equation} 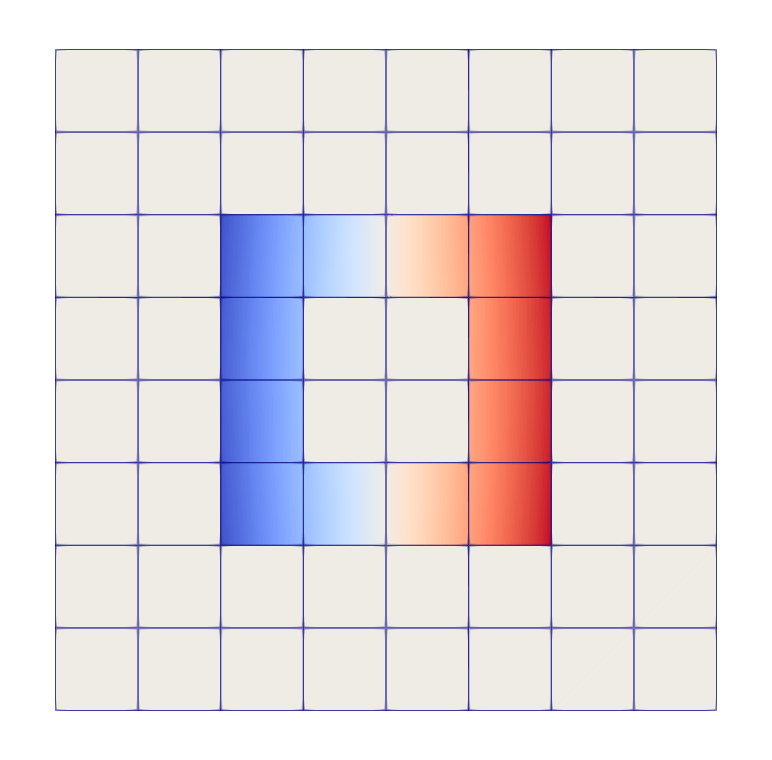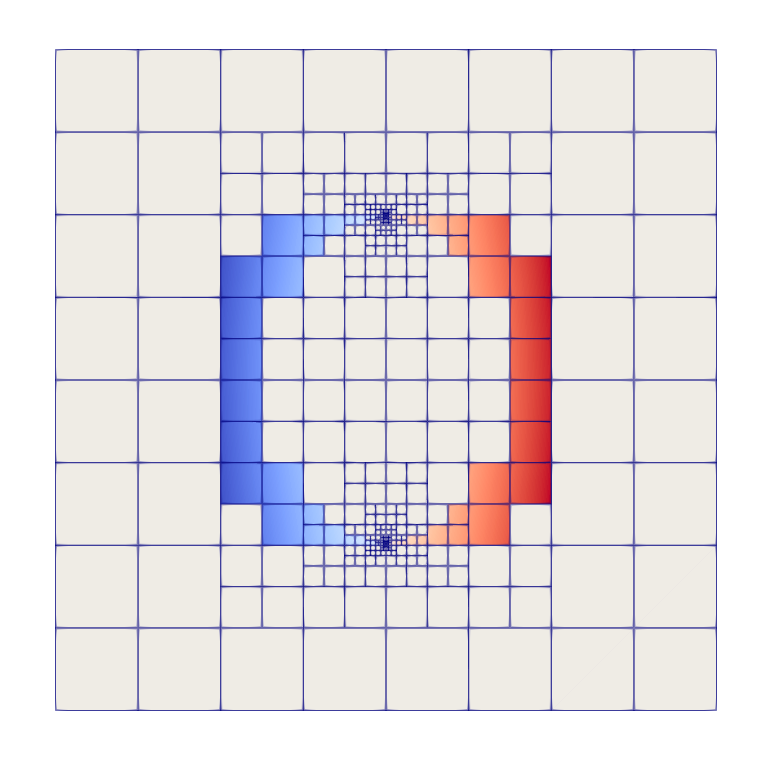We developed an unfitted method that relies on an uniform background mesh that allows for an arbitrary position of a curved boundary including its continuous deformations.

Targeted drug delivery

Numerical analysis of Allen-Cahn on evolving domains

The paper studies an Allen–Cahn-type equation defined on a time-dependent surface as a model of phase separation with order–disorder transition in a thin material layer. A geometrically unfitted finite element method, known as a trace FEM, is considered for the numerical solution of the equation. The paper provides full stability analysis and convergence analysis that accounts for interpolation errors and an approximate recovery of the geometry: $$\|\mathbb{E}^n\|^2_{\Gamma^{n}_{h}}+{\Delta t}\sum_{k=1}^{n} \|\nabla_{\Gamma_{h}}\mathbb{E}^k \|^2_{\Gamma^{k}_{h}} \lesssim \exp(c\, t_n) \|{u}\|_{W^{m+1,\infty}(\mathcal{G})}^2 (\Delta t^2+h^{2\min\{m,q\}})$$ Also, by a formal inner-outer expansion of the distance function, $d_\Gamma$, measured along the surface, it is shown that the limiting behavior of the solution $$\dot{d_\Gamma} = \mathop{\,\rm div_\Gamma} \nabla_\Gamma d_\Gamma \quad \text{on}~\Gamma(t)$$ which is a mean curvature flow generalized to the case of a time-dependent domain.

read

Cahn-Hilliard on evolving domains

The paper presents a model of lateral phase separation in a two component material surface. The resulting fourth order nonlinear PDE can be seen as a Cahn-Hilliard equation posed on a time-dependent surface. Only elementary tangential calculus and the embedding of the surface in $\mathbb{R}^3$ are used to formulate the model, thereby facilitating the development of a fully Eulerian discretization method to solve the problem numerically. A hybrid method, finite difference in time and trace finite element in space, is introduced and stability of its semi-discrete version is proved. The method avoids any triangulation of the surface and uses a surface-independent background mesh to discretize the equation. Thus, the method is capable of solving the Cahn-Hilliard equation numerically on implicitly defined surfaces and surfaces undergoing strong deformations and topological transitions. We consider a heterogeneous mixture of two species with densities $\rho_1$ and $\rho_2$. Let $c_1=\rho_1/(\rho_1+\rho_2)$ be the representative concentration $c$. By applying transport theorem and specifying a chemical potential we arrive at the following: $$\dot{c} - \rho^{-1}{\mathop{\,\rm div_\Gamma}} \left(M \nabla_\Gamma \left(\frac{1}{\epsilon}f_0' - \epsilon\Delta_\Gamma c\right)\right) = 0\quad \text{on}~\Gamma(t)$$ It is well known that in a steady domain the Cahn-Hilliard problem defines the $H^{-1}$-gradient flow of an energy functional.However, we are not aware of a minimization property for the Cahn-Hilliard problem in time-dependent domains. We demonstrate an energy bound $\text{for all}~n=1,\dots,N,$ assuming constant mobility: $$\frac{\epsilon}2\|\nabla_\Gamma c^{n}\|^2_{\Gamma_n} + \frac1{\epsilon}\int_{\Gamma_n} {f}_0(c^{n}) \, ds +\Delta t\sum_{k=1}^{n}\|\nabla_\Gamma \mu^k\|^2_{\Gamma_k} \le C({\rm data})$$

read

Surface Navier-Stokes

Fluid equations posed on manifolds naturally arise in mathematical models of lipid membranes, foams, emulsions and other thin material layers that exhibit surface fluidity and viscosity. The paper introduces a finite element method for the incompressible Navier--Stokes equations posed on a closed surface $\Gamma\subset\mathbb{R}^3$: $$\frac{\partial\mathbf{u}}{\partial t}+(\nabla_\Gamma \mathbf{u})\mathbf{u} - \nu\,\mathbf{P} {\mathop{\,\rm div}}_\Gamma (E_s(\mathbf{u}))+\nabla_\Gamma p = \mathbf{f} \,\, \text{on}~\Gamma$$ $$ {\mathop{\,\rm div}}_\Gamma \mathbf{u} =0 \quad \text{on}~\Gamma,$$ $$ \mathbf{u}\cdot \mathbf{n} =0 \quad \text{on}~\Gamma,$$ where $\mathbf{n}$ is the normal vector field, $E_s(\mathbf{u})=\nabla_\Gamma\mathbf{u}+\nabla_\Gamma^T\mathbf{u}$. The method needs a shape regular tetrahedra mesh in $\mathbb{R}^3$ to discretize equations on the surface, which can cut through this mesh in a fairly arbitrary way. Stability and error analysis of the fully discrete (in space and in time) scheme is given. The tangentiality condition for the velocity field on $\Gamma$ is enforced weakly by a penalty term. The paper studies both theoretically and numerically the dependence of the error on the penalty parameter. Several numerical examples demonstrate convergence and conservation properties of the finite element method. The main result is summarized in the following theorem. Assume $\Gamma\in C^3$ and the solution to the surface fluid system is sufficiently smooth such that holds. For the trace finite element method assume that the background mesh is quasi-uniform. Then the finite element method is stable and the following error estimate holds: $$\|\mathbb{E}_u^n\|^2+\sum_{k=1}^{n}\Delta t\left\{\|\mathbb{E}_u^k\|_{\mathbf{V}_\ast}^2+\|\mathbb{E}_p^k\|_{s}^2\right\} \leq$$ $$(1+\tau h^2)h^2+|\Delta t|^4+\tau^{-1}$$

read read

Phase-separation on surfaces

Conservative and non-conservative phase-field models are considered for the numerical simulation of lateral phase separation and coarsening in biological membranes. We consider Cahn-Hilliard model: $$\rho \frac{\partial c}{\partial t} - {\mathop{\,\rm div}}_\Gamma\left(M {\nabla{}}_\Gamma \mu \right) = 0 \quad \text{on}~\Gamma $$ $$\mu = f_0' - \epsilon^2 {\Delta}_\Gamma c \quad \text{on}~\Gamma$$ where $$f_0(c) = \frac{1}{4} (c -1)^2c^2$$ is the Ginzburg-Landau double-well potential and $$M(c)=c(1-c)$$ is the so-called mobility coefficient. An unfitted finite element method is devised for these models to allow for a flexible treatment of complex shapes in the absence of an explicit surface parametrization. For a set of biologically relevant shapes and parameter values, the paper compares the dynamic coarsening produced by conservative and non-conservative numerical models, its dependence on certain geometric characteristics and convergence to the final equilibrium. We obtain the weak (variational) formulation of the surface Cahn--Hilliard problem: Find $(c,\mu) \in H^1(\Gamma) \times H^1(\Gamma)$ such that $$ \int_\Gamma \rho \frac{\partial c}{\partial t} \,v \, ds + \int_\Gamma M \nabla_{\Gamma} \mu \, \nabla_{\Gamma} v \, ds = 0, $$$$ \int_\Gamma \mu \,q \, ds - \int_\Gamma f_0'(c) \,q \, ds - \int_\Gamma \epsilon^2 \nabla_{\Gamma} c \, \nabla_{\Gamma}q \, ds = 0, $$ for all $(v,q) \in H^1(\Gamma) \times H^1(\Gamma)$. After validating the accuracy of our implementation of TraceFEM with benchmark problems, we applied it to simulate phase transition on a series of surfaces of increasing geometric complexity using both the surface Allen--Cahn and Cahn--Hilliard models. We compared the numerical results produced by the two models on a sphere and found that the Cahn--Hilliard model successfully reproduces the spinodal decomposition experimentally observed in giant vesicles. Both models were also compared on the surface of a spindle with the aim of getting a preliminary insight into the formation of microdomains in bacteria. Finally, we presented the results on a more complex surface that represents an idealized cell. For both the sphere and the idealized cell, we let the simulations run until sufficiently close to the steady state to understand the role of certain geometric characteristics on the final equilibrium.

read

Thermoreactive transport

Multispecies thermodynamics

Numerical modeling of reactive media composed of different species is very challenging due to various reasons: stiffness due to fast chemical reactions, high gradients of temperature field and nonconstant heat capacities. Mathematical models need to be physically relevant and computationally efficient at the same time. Here we derive thermodynamically correct transport equations for thermoreactive mixture flows and provide with a numerically favourable formulation. $$\frac{\partial{}c_k}{\partial{}t} + \nabla{}\cdot{}\left(c_k \vec{U}_k(\vec{x},t) - D_k(T) \nabla{}c_k \right) = \sum_r I_r(c_1,..,c_N, T) \nu^r_k$$ $$ \sum_k c_k C_k(T) \frac{\partial{} T }{\partial{}t} + \underbrace{ \sum_k C_k(T) \left( c_k\vec{U}_k(\vec{x},t) - D_k(T) \nabla{}c_k\right) \cdot{} \nabla{} T}_{ \mbox{advective term} }= $$ $$= \nabla{} \cdot{} \left( \sum_k \frac{ K_k(T) c_k \mu_k}{\sum_j c_j \mu_j } \nabla T \right) - \sum_r I_r(c_1,..,c_N, T) \Delta{}H_r(T) + q^{ext} $$ Conservative forms of equations are very desirable in numerical simulations but it relies on precise knowledge of partial enthalpies values including enthalpies of formation of all the species. It could be a problem in case when only apparent heat capacities and chemical reaction enthalpies are known. The thermal energy equation can be converted into equivalent almost conservative form: $$ \sum_k c_k C_k(T) \frac{\partial{} T }{\partial{}t} + T \sum_k C_k(T) \frac{\partial{}c_k}{\partial{}t} + \nabla{} \cdot{} \left( T \sum_k C_k(T) \left( c_k\vec{U}_k(\vec{x},t) - D_k(T) \nabla{}c_k\right) \right) -$$$$- T \nabla{} T \cdot{} \sum_k \left( c_k\vec{U}_k(\vec{x},t) - D_k(T) \nabla{}c_k\right) \frac{dC_k(T) }{dT} = \nabla{} \cdot{} \left( \sum_k \frac{ K_k(T) c_k \mu_k}{\sum_j c_j \mu_j } \nabla T \right) -$$$$- \sum_r I_r(c_1,..,c_N, T) \left( \Delta{}H_r(T) - T C_k(T) \nu_k^r\right) + q^{ext}$$ This form of thermal energy equation is numerically preferable if number of species in a mixture is large.