

The selection structure is used to make a comparison between two values and uses the results to determine the next action to be taken. In FORTRAN, the IF statement, containing a logical comparison is used in the selection structure. There are two main forms of the IF structure: a logical IF statement and a block IF.

As shown in Figure 1, if logical exp. is true, statement 1 is executed and then next statement is executed. If logical exp. is false, statement 1 is ignored and next statement is executed. Example
The block IF structure is used when more than one statement (referred to as a block of statements) is to be executed. Its general form is
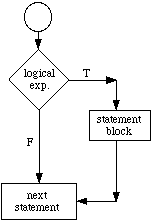
As shown in Figure 2, if logical exp. is true, then statement block will be executed. If logical exp. is false, program control immediately passes to next statement and statement block is not executed.
Example
c The following program reads the name of a student and the student's gpa.
c If the gpa is greater than or equal to 3.5, the student's name and gpa are
c printed. The number of honor students, students with gpa's greater
c than or equal to 3.5, is also incremented and printed when the user has
c finished entering names.
PROGRAM honor
REAL gpa
INTEGER honor
CHARACTER name*20, answer*1
honor = 0
5 PRINT *, 'Student"s name:'
READ *,name
PRINT *, 'GPA: '
READ *, gpa
IF (gpa .ge. 3.50) THEN
PRINT *,name, ' is an honor roll student with GPA: 'gpa
honor = honor + 1
ENDIF
PRINT *, 'Do you want to enter another name (y=yes, n=no)?'
READ *, answer
IF (answer .eq.'y') go to 5
PRINT *, 'The number of honor roll students is ', honor
END
If the value of the variable gpa is greater than or equal to 3.50, the program prints the student's name and gpa and adds one to the current value of the variable honor. If the value of the variable gpa is less than 3.50, the student's name and gpa is not printed and program control passes to the PRINT statement following the END IF. Notice that the logical IF statement is used to allow the user to enter an arbitrary number of student names and associated GPA's.
Example - Division Program 1
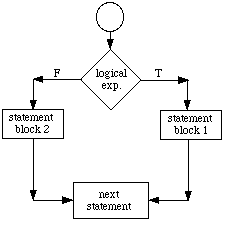
Figure 3 illustrates that if the logical expression is true,
statement block 1 is executed. If it is false,
statement block 2 is executed.
Example - Division Program 2
The division program could have been written with an IF-THEN-ELSE
structure.
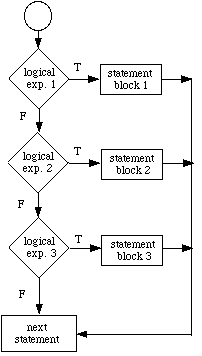
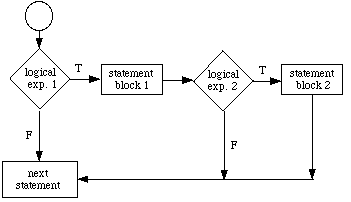
As shown in Figure 4, if logical exp. 1 is true, statement
block 1 is executed and program control passes to next
statement. If logical exp. 1 is false and logical
exp. 2 is true, then statement block 2 is
executed and program control passes to next statement. Likewise, if the
first two logical statements are false and
logical exp. 3 is true, statement block 3 is executed and
program control passes to next statement . The
statement block following the first logical expression which is true is the
only statement block that will be executed. If none of the logical
expressions is true, program control passes to the next statement
following the END IF.
Example - Number of Distinct Real Roots in a Quadratic Equation
IF statements may also be nested within IF statements. They then
take the general form
Enter, compile, and execute the program. Give the output when
2. Pythagorean Triple Program
Give the output for the program when
What determines which lines of the program are executed?
This program places an object in a shipping category when the weight
of the object is entered. Weights and categories are listed in
Table 1.
Enter, compile, and execute the program.
Give the output for the program when
Why do the results change? What determines which lines of the program
are executed?
The brightness of a binary star varies in a cycle with a 6.4 day
period.
Write a program that calculates the magnitude of a binary star given
the time
in the cycle.
The mathematical model for this
program has already been developed. It uses the
intrinsic functions ln and cos. Note that pi
is a
variable and must be assigned a value. The times and magnitudes are
listed in
Table 2.
IF-THEN-ELSE IF Structure
The IF-THEN-ELSE IF structure is an extension of the
IF-THEN-ELSE structure. The added feature is the ability to handle multiple
conditions. Its general form for three conditions is
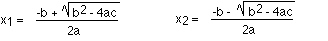
Nested IF Statements
EXERCISES
1. Number of Real Roots in a Quadratic Equation
Program
Notice the flow of the program based on the value of the variable rad
and the nested IF-THEN-ELSE structure.
Write a program (on paper) implementing the algorithm.
3. Shipping Category Program
Weight
Category
0.0 =< weight < 21.0
1
21.0 =< weight < 101.0
2
101.0 =< weight < 201.0
3
201.0=< weight < 301.0
4
301.0 =< weight
5
Time (days)
Magnitude
0.0 =< time < 0.9
2.5
0.9 =< time < 2.3
3.355 - ln(1.352 + cos(pi(t - 0.9)/0.7))
2.3 =< time < 4.4
2.5
4.4 =< time < 5.2
3.598-ln(1.998 + cos(pi(t - 4.4)/0.4))
5.2 =< time < 6.4
2.5
Determine the values for the magnitude using a calculator or the data
provided in the table when time = .6, 1.0, 3.0, 5.0, 6.0.
Test the program using your data.



